Show that the locus of the mid-points of all chords passing through the vertices of the parabola $y^{2}$ =4ax is the parabola $y^{2} = 2 a x$ .

Video Solution

Text Solution

Verified by Experts

Let AP be a chord of parabola $y^{2} = 4 a x$ which passes through the vertex A and the co-ordinates of point P be $(x_{1}, y_{1})$ .

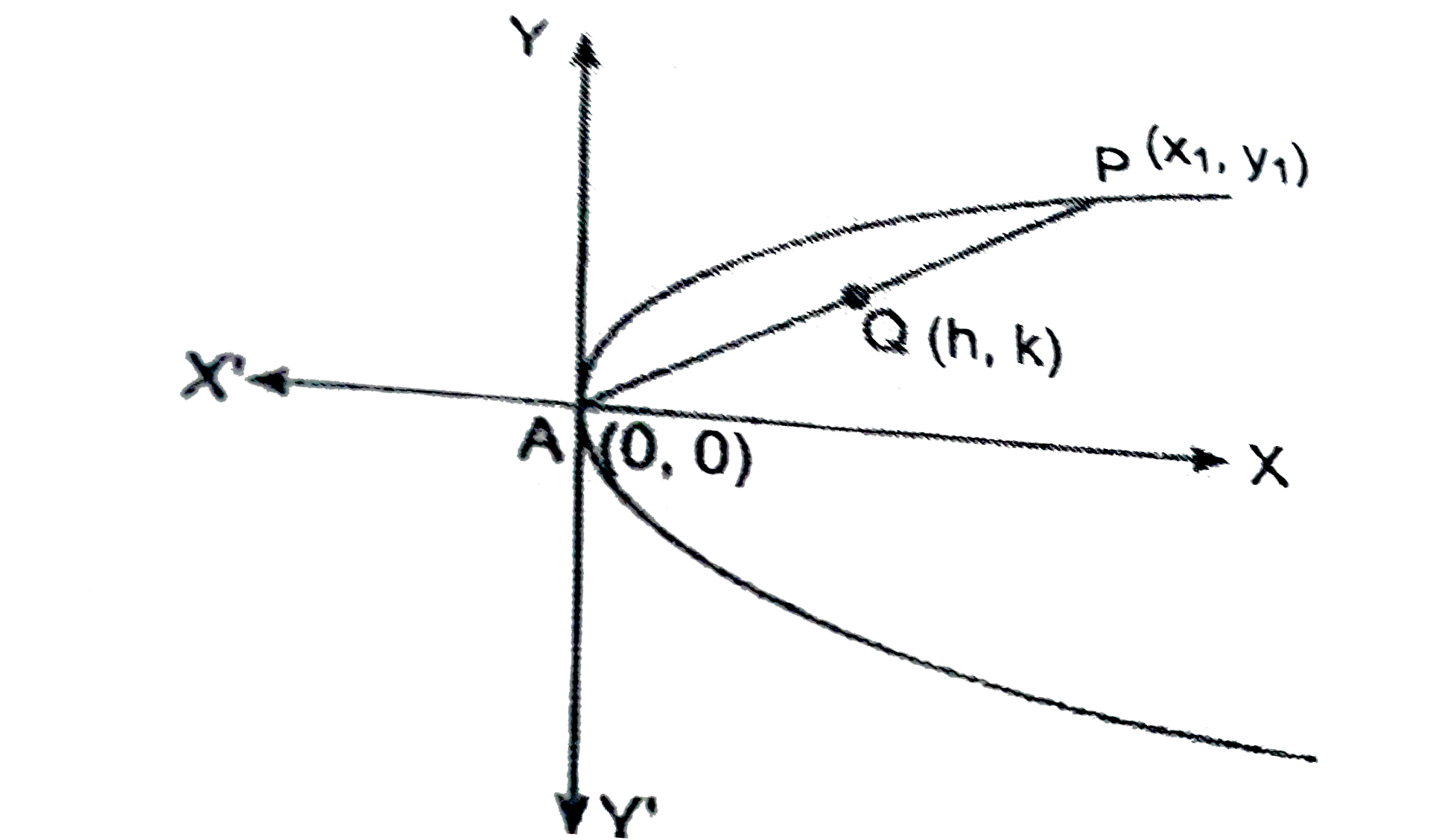
Point $P (x_{1}, y_{1})$ lies on the parabola $y^{2} = 4 a x$ .
$∴ y_{1}^{2} = 4 a x_{1}$ . . .(1)
Let Q be the mid point of AP and its co-ordinates are
(h,k).
$∴ h = \frac{0 + x_{1}}{2} and k = \frac{0 + y_{1}}{2}$
$\Rightarrow x_{1} = 2 h and y_{1} = 2 k$
From eq. (1)
${(2 k)}^{2} = 4 a (2 h)$
$\Rightarrow k^{2} = 2 a h$
$∴$ Locus of Q(h, k)
$y^{2} = a x$ .

Updated on:21/07/2023

IF (a,b) is the mid point of chord passing through the vertex of the parabola $y^{2} = 4 x$ , then
Aa=2b
B2a=b
C $a^{2} = 2 b$
D $2 a = b^{2}$
Find the locus of the middle points of the chords of the parabola $y^{2} = 4 x$ which touch the parabola $x^{2} = - 8 y$ .
A $y^{3} - 2 x y - 8 = 0$
B $y^{3} + 2 x y - 8 = 0$
C $y^{3} - 2 x y + 8 = 0$
D $y^{3} - x y - 8 = 0$
The locus of the middle points of all chords of the parabola $y^{2} = 4 a x$ passing through the vertex is
Aa straight line
Ban ellipse
Ca parabola
Da circle