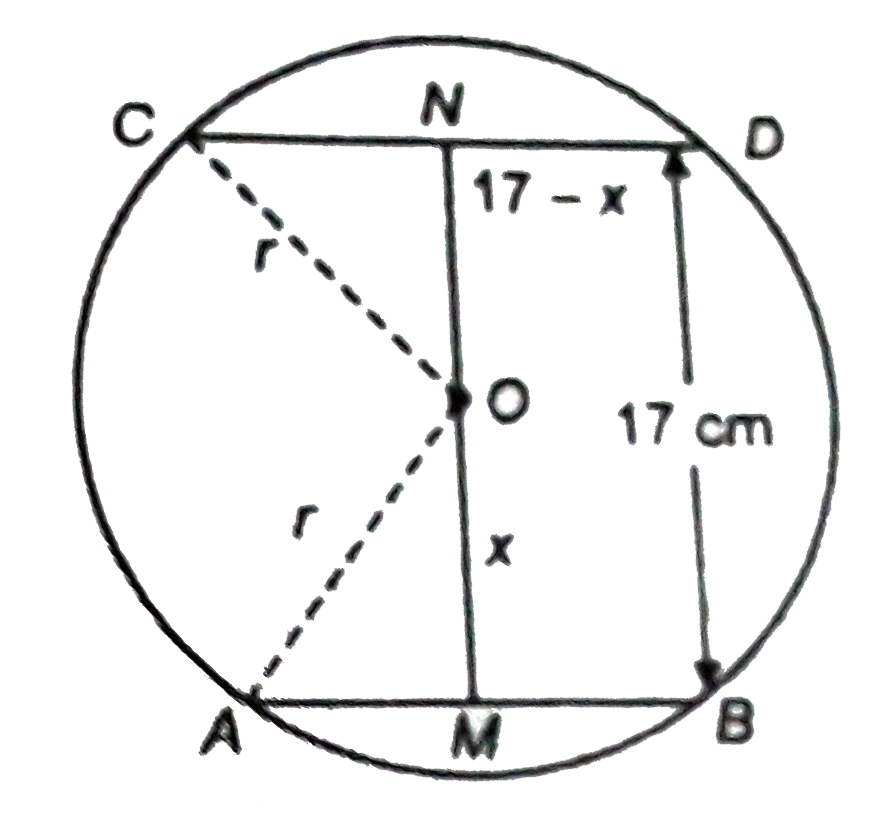
AB and CD are two parallel chords of a circle which are on opposite sides of the centre such that AB=10 cm, CD=24 cm and the distance between AB and CD is 17 cm.Find the radius of the circle.

Video Solution

Text Solution

Verified by Experts

In the adjoining figure, O is the centre of the circle.
Here, $A B = 10 c m$
$C D = 24 c m$
OM and ON are perpendicular from centre $O$ to AB and CD respectively.
$∵ A B ∣ ∣ C D$
$∴$ MON is a transversal
Now, $A M = \frac{1}{2} A B = \frac{1}{2} \times 10 = 5 c m$
$C N = \frac{1}{2} C D = \frac{1}{2} \times 24 = 12 c m$
Let $O M = x$
$∴ O N = 17 - x$
In $Δ O M A$ ,
$O A^{2} = O M^{2} + A M^{2}$ (where $O A = r$ is the radius of circle)
$\Rightarrow r^{2} = x^{2} + 5^{2}$ ........(1)
$∴$ In $Δ O C N$ ,
$O C^{2} = O N^{2} + C N^{2}$
$\Rightarrow e^{2} = {(17 - x)}^{2} + 12^{2}$ .........(2)
From eqs. (1) and (2).
$x^{2} + 5^{2} = {(17 - x)}^{2} + 12$
$\Rightarrow x^{2} + 25 = 289 + x^{2} - 34 x + 144$
$\Rightarrow 34 x = 289 + 144 - 25$
$= 408$
$\Rightarrow x = \frac{408}{34} = 12$
Put $x = 12$ in eq. (1)
$r^{2} = x^{2} + 5^{2}$
$= 12^{2} + 5^{2}$
$= 144 + 25$
$= 169$
$\Rightarrow r = \sqrt{169} = 13 c m$
$∴$ Radius of circle =13cm.

Updated on:21/07/2023

$A B$ and $C D$ are two parallel chords of a circle which are on opposite sides of the centre such that $A B$ $= 10 c m$ , CD $= 24$ cm and the distance between $A B$ and $C D$ is $17 c m .$ Find the radius of the circle.
A $13$ cm
B $14$ cm
C $15$ cm
D $16$ cm
AB and CD are two chords of a circle such that AB = 10 cm, CD - 24 cm and AB||CD. If the distance between AB and CD is 17 cm. Then, the radius of the circle is equal to
A13
B169
C26
Dnone of these
AB and CD are two chords of a circle such that AB= 10 cm, CD = 24 cm and AB|| CD. The distance between AB and CD is 17 cm. Then, the radius of the circle is equal to
A13cm
B169cm
C26cm
Dnone of these