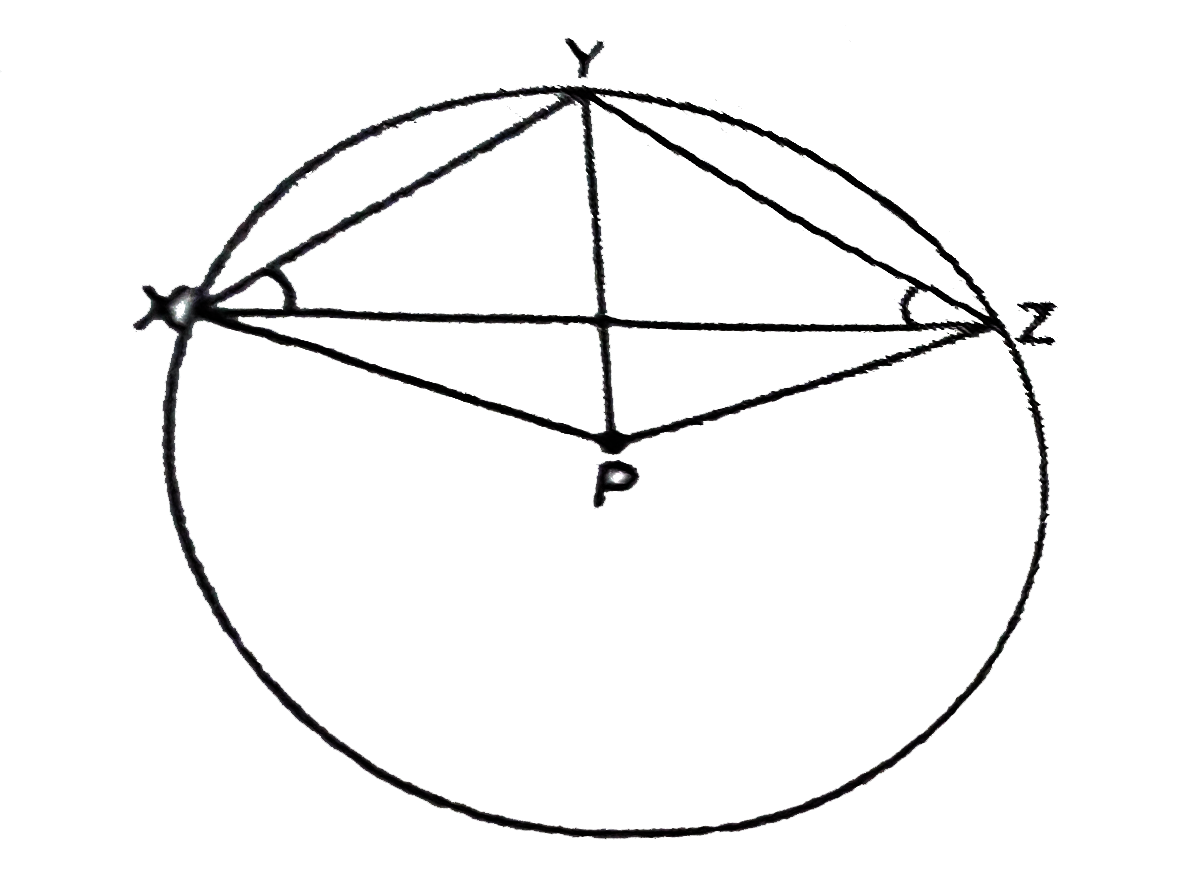
In the figure, P is the centre of the circle. Prove that : ∠XPZ=2(∠XZY+∠YXZ).

Video Solution
Text Solution
Since, arc XY subtends ∠XPY at the centre and ∠XZY at a point Z in the remaining part of the circle.
∴∠XPY=2∠XZY ........(1)
Similarly, arc YZ subtends ∠YPZ at the centre and ∠YXZ at a point X in the remaining part of the circle.
∴∠YPZ=2∠YXZ
Adding eqs. (1) and (2) , we have
∠XPY+∠YPZ=2∠XZY+2∠YXZ
⇒∠XPZ=2(∠XZY+∠YXZ)
|
Topper's Solved these Questions
- CIRCLE BOOK - NAGEEN PRAKASHANCHAPTER - CIRCLE EXERCISE - Exercise 10a
22 Videos
- CIRCLE BOOK - NAGEEN PRAKASHANCHAPTER - CIRCLE EXERCISE - Exercise 10b
19 Videos
- AREA OF PARALLELOGRAMS AND TRIANGLESBOOK - NAGEEN PRAKASHANCHAPTER - AREA OF PARALLELOGRAMS AND TRIANGLESEXERCISE - Revision Exercise (long Answer Question)
5 Videos
- CO-ORDINATE GEOMETRY BOOK - NAGEEN PRAKASHANCHAPTER - CO-ORDINATE GEOMETRY EXERCISE - Exercise
8 Videos
Similar Questions
Knowledge Check
In the adjoining figure, O is the centre of the circle, Then x=?
 Az+yBz−yCy−zDnone of these
Az+yBz−yCy−zDnone of theseIn the figure, O is the centre of the circle . ∠PQR is equal to
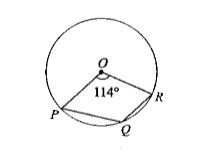 A57∘B63∘C123∘D92∘
A57∘B63∘C123∘D92∘In the given figure, O is the centre of the circle. Then ∠AED measure
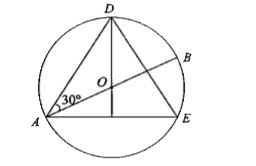 A30∘B45∘C60∘D90∘
A30∘B45∘C60∘D90∘
In the figure, P is the centre of the circle. Prove that: ∠XPZ=2 (∠XZY+ ∠YXZ)
View SolutionIn figure O is the centre of the circle, prove that ∠z=∠x+∠y.

View SolutionIn Figure, O is the centre of the circle, prove that ∠x=∠y+∠z
View SolutionP is the centre of the circle prove that ∠XPZ=2(∠XZY+∠YXZ)
View SolutionIn the figure, O is the centre of the circle. Prove ∠AOC=∠AFC+∠AEC.
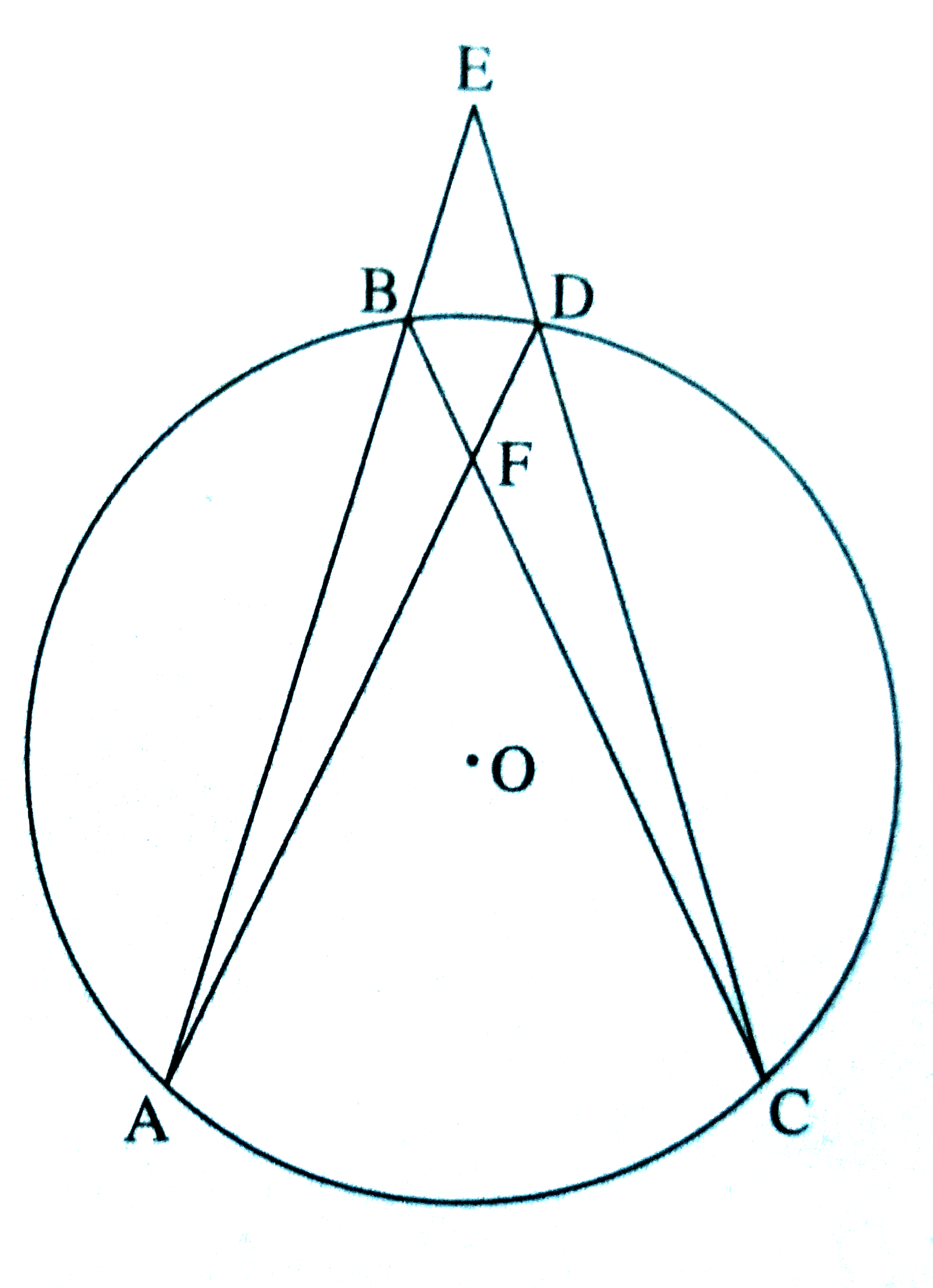
View Solution