The taxi fare in a city is as follows: For the first kilometre, the fare is Rs 8 and for the subsequent distance it is Rs 5 per km. Taking the distance covered as x km and total fare as Rs y, write a linear equation for this information, and draw.
Distance covered = x Km =1 + (x-1) Km fare for first kilometre = Rs 8 fare for next (x-1) km=Rs(x-1)xx5=Rs 5(x-1)
According to question total fare =Rs y
8+5(x-1)=y⇒ 8+5x-5=y ⇒ 5x-y+3=0
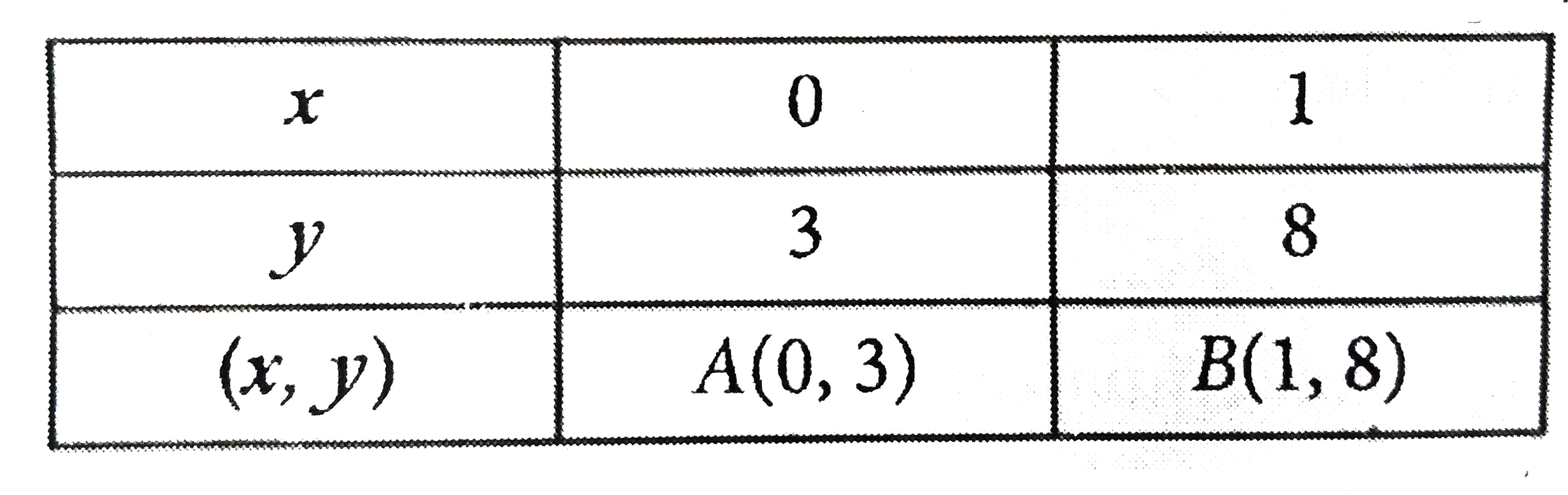
Now plot the points A(0,3) and B(1,8) on a graph paper and joining tghem to form a line AB.
Topper's Solved these Questions
- LINEAR EQUATIONS IN TWO VARIABLESBOOK - NAGEEN PRAKASHANCHAPTER - LINEAR EQUATIONS IN TWO VARIABLESEXERCISE - Exercise
3 Videos
- LINEAR EQUATIONS IN TWO VARIABLESBOOK - NAGEEN PRAKASHANCHAPTER - LINEAR EQUATIONS IN TWO VARIABLESEXERCISE - Revision Exercise
12 Videos
- LINEAR EQUATIONS IN TWO VARIABLESBOOK - NAGEEN PRAKASHANCHAPTER - LINEAR EQUATIONS IN TWO VARIABLESEXERCISE - Revision Exercise
12 Videos
- INTRODUCTION TO EUCLID'S GEOMETRYBOOK - NAGEEN PRAKASHANCHAPTER - INTRODUCTION TO EUCLID'S GEOMETRYEXERCISE - Exercise
3 Videos
- LINES AND ANGLESBOOK - NAGEEN PRAKASHANCHAPTER - LINES AND ANGLESEXERCISE - Revision Exercise (long Answer Questions )
6 Videos
Similar Questions
The taxi fare in a city is as follows: For the first kilometer, the fare is Rs.8 and for the subsequent distance it is Rs 5 per km. Taking the distance covered as x km and total fare as Rs. y, writes a linear equation for this information, and draw its graph.
View SolutionThe taxi fare in a city is as follows: For the first kilometer, the fare is Rs.8 and for the subsequent distance it is Rs 5 per km. Taking the distance covered as x km and total fare as Rs. y, writes a linear equation for this information, and draw its graph.
View SolutionThe taxi fare in a city is charged according to the rates stated as : For the first 3 km distance, the fare is Rs. 10 (even for less than 3 km) and for the subsequent distance is Rs.4 per km. Taking the distance covered as x km and total fare as Rs. y, write a linear equation for the above and draw its graph From the graph, find the distance travelled when the amount paid is Rs. 60.
View SolutionA taxi charges .Rs 20 for the first kilometre and @12 .Rs per km for subsequent distance covered. Taking the total distance covered as x km and total fare .Rs y, write a linear equation depicting the relation between x and y. Draw the graph between x and y.
Form your graph, find the taxi charges for covering
(a) 12 km and (b) 20 km.
View SolutionAn auto rickshaw charges Rs 10 for the first kilometre then Rs 8 for each such subsequent kilometre. The total charge (in Rs) for d kilometres is
View SolutionaA three-wheeler scooter charges 15 for first kilometer and 8 each for every subsequent kilometer. For a distance of x km, an amount of y is paid. Write the equation representing the above information
View SolutionThe parking charges of a car in a private parking is Rs 20 for the first hour and Rs 10 for subsequent hours.Taking total parking charges to be y & total parking time as x hours form a linear equation.Write it in standard form.
View SolutionThe taxi fare after each km when the fare is Rs 15 for the first km and Rs 8 for each additional km
View SolutionThe railway fare for 61 km is Rs 183. Find the fare for 53 km.
View SolutionIt is common that Governments revise travel fares from time to time based on various factors such as inflation ( a general increase in prices and fall in the purchasing value of money) on different types of vehicles like auto, Rickshaws, taxis, Radio cab etc. The auto charges in a city comprise of a fixed charge together with the charge for the distance covered. Study the following situations

Situation 1: In city A, for a journey of 10 km, the charge paid is Rs 75 and for a journey of 15 km, the charge paid is Rs 110.
Situation 2: In a city B, for a journey of 8km, the charge paid is Rs91 and for a journey of 14km, the charge paid is Rs 145.
If the fixed charges of auto rickshaw be Rs x and the running charges be Rs y km/hr, the pair of linear equations representing the situation is
View Solution
