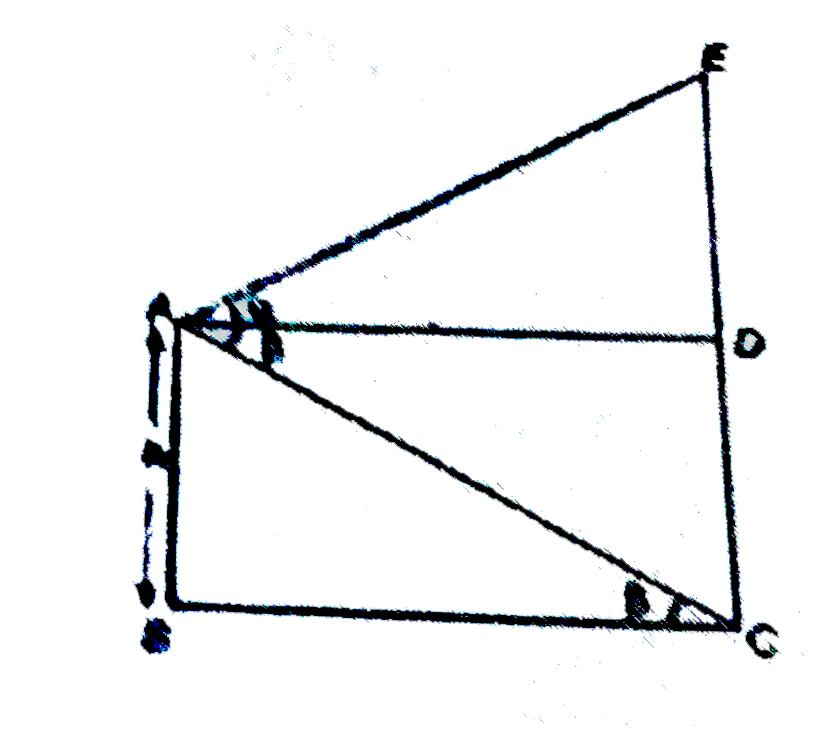
From a window ( h meter above ground) the angle of elevation of other house is $θ$ and angle of depression is $ϕ$ . Find the height of the house.

Video Solution

Text Solution

Verified by Experts

Let A be the window of a house of height 'h'. CE be another house in front of first house.
Given that
$∠ E A D = α and ∠ A C B = β$
In $Δ A E D$ ,
$cot β = \frac{B C}{A B} = \frac{B C}{h} \Rightarrow B C = h cot β \dots (1)$
In $Δ A E D$ ,
$tan α = \frac{E D}{A D} \Rightarrow tan α = \frac{E D}{B C} \Rightarrow tan α = \frac{E D}{B C}$
$\Rightarrow E D = B C tan α = h tan α cot β$
Now $E C = D C + E D = h + h tan α cot β$
$= (1 + tan α cot β)$
$∴ Height of other house = h (1 + tan α cot β)$

|

Updated on:21/07/2023

Class 10 MATHS SOME APPLICATIONS OF TRIGONOMETRY

Topper's Solved these Questions

Similar Questions

Knowledge Check

Question 1 - Select One
From the top of a 10 m high building, the angle of elevation of the top of a tower is $60^{\circ}$ and the angle of depression of its foot is $45^{\circ}$ . Find the height of the tower
A17.42
B27.32 m
C23.62 m
Dnone to these
Question 2 - Select One
From a window (h m high above the ground) of a house in a street, the angle of elevation and depression of the top and the foot of another house on the opposite side to the street are and 0, respectively. Then, the height of the opposite house is
A $h cot θ cot ϕ$
B $h (cot θ cot ϕ + 1)$
C $h tan θ cot ϕ$
D $h (tan θ cot ϕ + 1)$
Question 3 - Select One
The angle of elevation of a cloud from a height h above the level of water in a lake is $α$ and the angle of depressionof its image in the lake is $β$ . Find the height of the cloud above the surface of the lake:
A $\frac{h sin (β - α)}{sin (α + β)}$
B $h sin α$
C $\frac{h sin (α + β)}{sin (β - α)}$
Dnone of these

NAGEEN PRAKASHAN-SOME APPLICATIONS OF TRIGONOMETRY-Long Answer Questions

Home
Ask Doubt
Profile