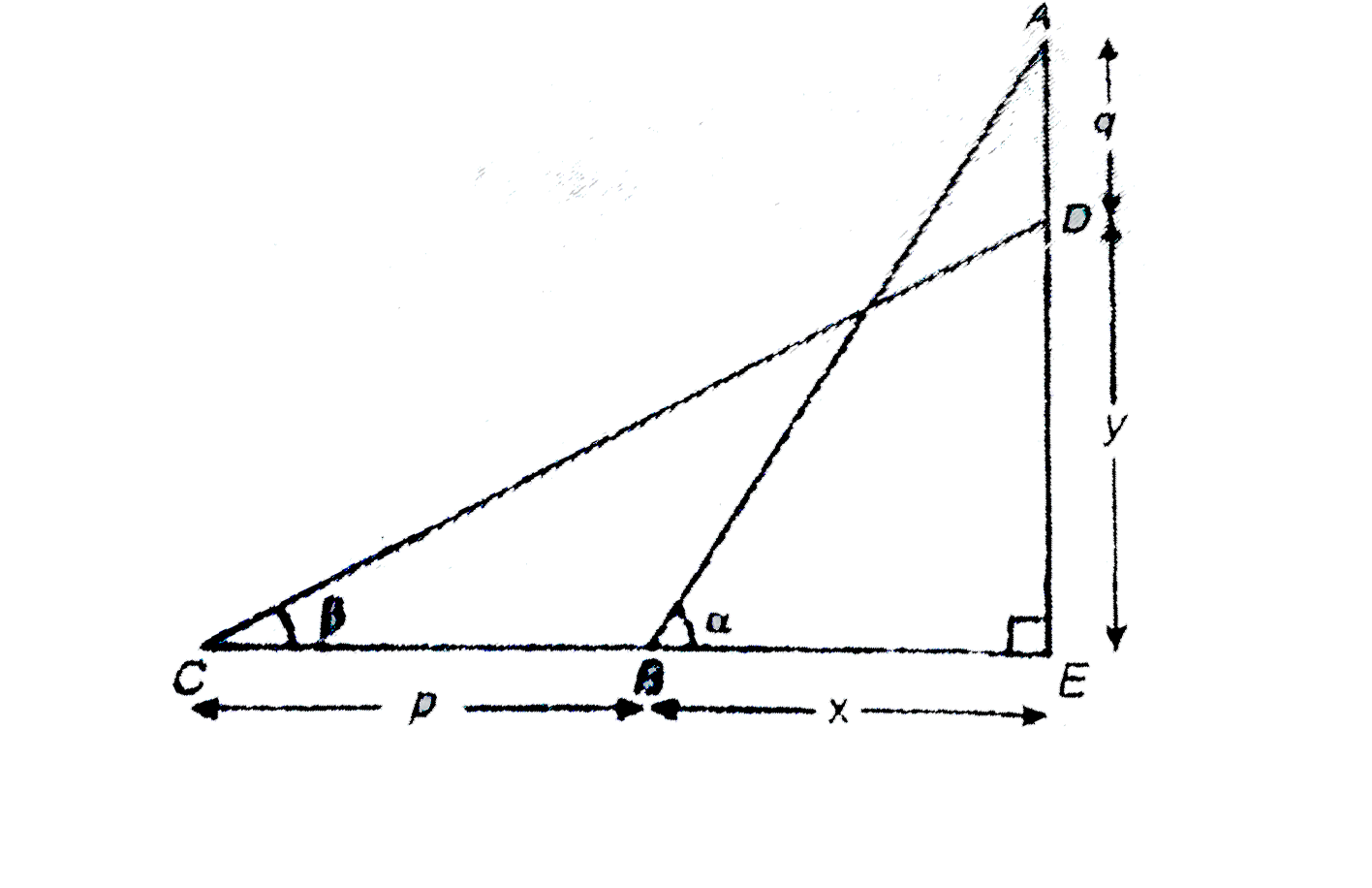
A ladder rests against a vertical wall at inclination α to the horizontal. Its foot is pulled away from the wall through a distance p so that it's upper end slides q down the wall and then ladder make an angle β to the horizontal show that pq=cosβ−cosαsinα−sinβ.
Let a ladder AB of lengt 'l', resting against the wall such that ∠ABE=α
when its foot pulled away from the wall at a distance 'p' then new position of the ladder becomes CD.
Now, CD=AB=l
Given that, ∠DCE=β and AD=q
Let BE=x and DE=y
In ΔABE,
sinα=AEAB=q+y1 and cosα=BEAB=xl
In ΔCDE,
sinβ=DECD=y1 and cosβ=CECD=p+xl
Now, cosβ−cosα=p+xl−xl=pl...(1)
and sinα−a∈β=q+yl−xl=q1...(2)
Divide equation (1) by equation (2), we get
cosβ−cosαsinα−sinβ=p/lq/l=pq
Topper's Solved these Questions
- SOME APPLICATIONS OF TRIGONOMETRYBOOK - NAGEEN PRAKASHANCHAPTER - SOME APPLICATIONS OF TRIGONOMETRYEXERCISE - Exercise
32 Videos
- SOME APPLICATIONS OF TRIGONOMETRYBOOK - NAGEEN PRAKASHANCHAPTER - SOME APPLICATIONS OF TRIGONOMETRYEXERCISE - Revision Exercise (short Answer Questions)
5 Videos
- REAL NUMBERSBOOK - NAGEEN PRAKASHANCHAPTER - REAL NUMBERSEXERCISE - Revision Exercise Long Answer Questions
5 Videos
- STATISTICS BOOK - NAGEEN PRAKASHANCHAPTER - STATISTICS EXERCISE - Revision Exercise Long Answer Questions
5 Videos
Similar Questions
A ladder rests against a wall at an angle α to the horizontal, its foot is pulled away from the wall through a distance a, so that it slides a distance b down the wall making an angle β with the horizontal. Show that a=btan12(α+β).
View Solutionladder rests against a wall at an angle α to the horizontal its foot pulled away from the wall through a distance a so that it slides a distance b down the wall making an angle β with the horizontal. Show that ab=cosα−cosβsinβ−sinα
View Solution
Knowledge Check
A ladder rests against a vertical wall at angle α to the horizontal . If is foot is pulled away from the wall through a distance 'a' so that it slides a distance 'b' down the wall making the angle β with the horizontal , then a =
Abtan(α−β2)Bbtan(α+β2)Cbcot(α−β2)Dnone of theseA ladder rests against a vertical wall at angle α to the horizontal . If is foot is pulled away from the wall through a distance 'a' so that it slides a distance 'b' down the wall making the angle β with the horizontal , then a =
Aa=b tanα+β2Ba=b cotα+β2Catan(α−β)2DNoneA ladder rests against a wall at an acute angle α to the horizontal. Its foot is pulled away form the wall through a distance 2 m, so that it slides a distance 3 m down the wall making an acute angle β with the horizontal , then the value of tan(α+β2) is
A32B23C49D94
A ladder rest against a wall making an angle α with the horizontal. The foot of the ladder is pulled away from the wall through a distance x, so that it slides a distance y down the wall making an angle β with the horizontal. Prove that x=ytan(α+β)2.
View SolutionA ladder rests against a wall making an angle alpha with the horizontal. The foot of the ladder is pulled away from the wall through a distance x so that it slides a distance y down the wall making an angle beta with the horizontal.The correct relation is (A) x=y tan(alpha+beta)/(2) (B) y=x tan(alpha+beta)/(2) (C) x=y tan(alpha+beta) (D) y=x tan(alpha+beta) (in)
View SolutionA ladder rests against a wall making an angle alpha with the horizontal. The foot of the ladder is pulled away from the wall through a distance x so that it slides a distance y down the wall making an angle beta with the horizontal.The correct relation is (A) x=y tan(alpha+beta)/(2) (B) y=x tan(Q+beta)/(2) (c) x=y tan(alpha+beta) (0) y=x tan(alpha+beta) (a)
View SolutionA ladder rests against a wall making an angle α with the horizontal. The foot of the ladder is pulled away from the wall through a distance ‘a’ so that it slides a distance ‘b’ down the wall making an angle beta with the horizontal then the value of ab is
View SolutionA ladder rests against a vertical wall at an angle α to the horizontal. If the foot is pulled away through a distance 2m, then it slides a distance 5 m down the wall, finally making an angle β with the horizontal. The value of tan(α+β2) is equal to
View Solution
