The angle of elevation of the top of a tower from two distinct points s and t from foot are complementary. Prove that the height of the tower is $\sqrt{s t}$ .

Video Solution

Text Solution

Verified by Experts

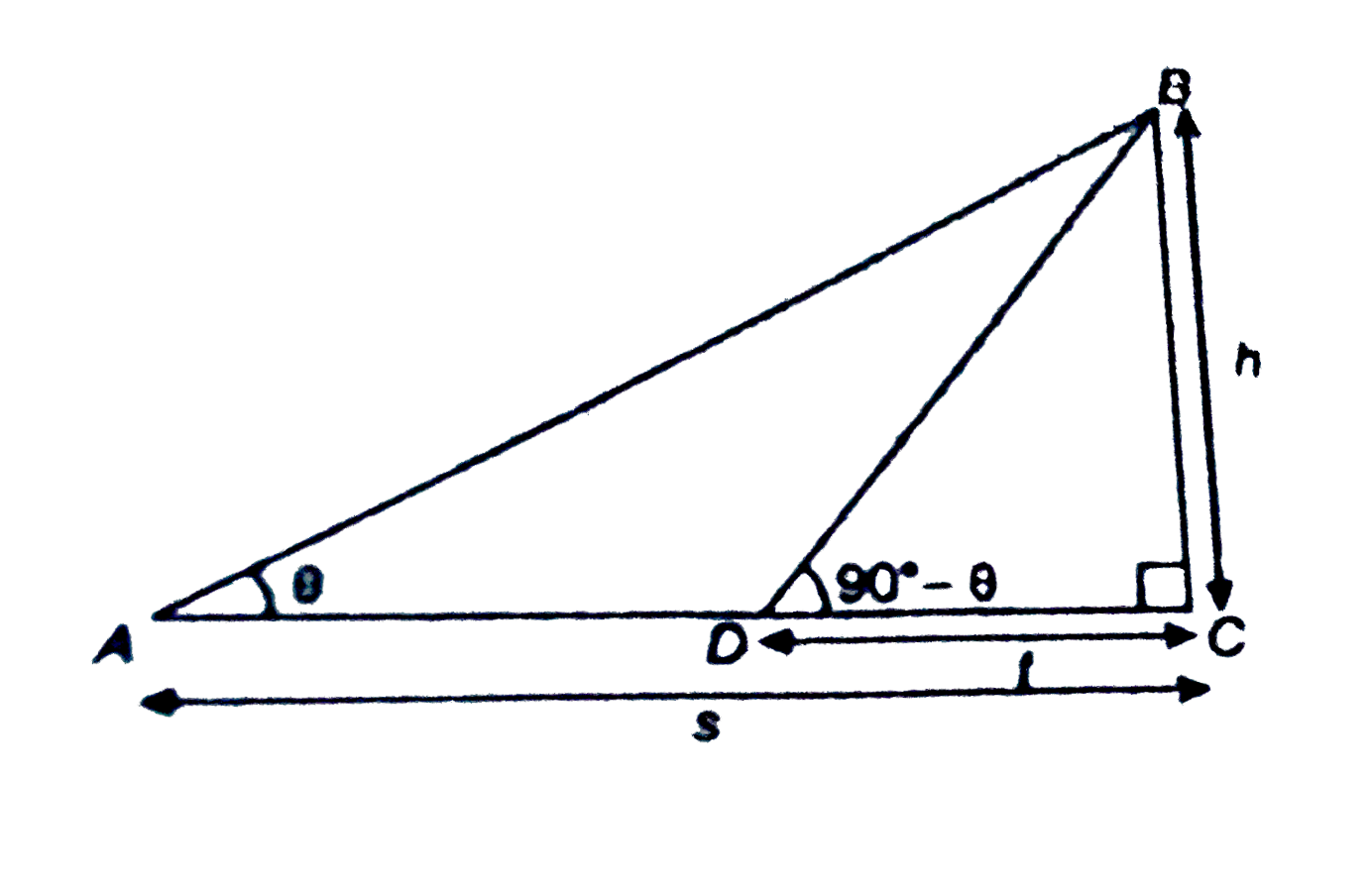
Let BC be a tower of height 'h'. Let $A C = s and D C = t$ . From points A and D, the angle of elevation of top B of the tower are complementary.
Let $∠ B A C = θ$
$∴ ∠ B D C = 90^{\circ} - θ$
In $Δ B A C$
$tan θ = \frac{B C}{A C} = \frac{h}{s} \dots (1)$
In $Δ B D C$
$tan (90^{\circ} - θ) = \frac{B C}{C D} \Rightarrow cot θ = \frac{h}{t}$
$\Rightarrow \frac{1}{tan θ} = \frac{h}{t} \Rightarrow \frac{s}{h} = \frac{h}{t} [o m (1)]$
$\Rightarrow h^{2} = s t \Rightarrow h = \sqrt{s t}$
$∴ height of the tower = \sqrt{s t}$

Updated on:21/07/2023

If the angles of elevation of the top of a tower from two points distance s and $t (s > t)$ from its foot are 30° and 60° respectively, then the height of the tower is
A $\sqrt{s + t}$
B $\sqrt{s t}$
C $\sqrt{s - t}$
D $\sqrt{\frac{s}{t}}$
The angle of elevation from two points at a distance of x and y from the feet of a Tower are complementary, the height of the Tower is
A $\sqrt{x y}$
B $\frac{x}{y}$
C $\sqrt{\frac{x}{y}}$
D $\sqrt{x + y}$
The angle of elevation of the top of a tower from the point P and Q at distance of a and b respectively from the base of the tower and in the same straight line with it are complementary .The height of the tower is
A $\sqrt{a b}$
B $\frac{a}{b}$
Cab
D $a^{2} b^{2}$