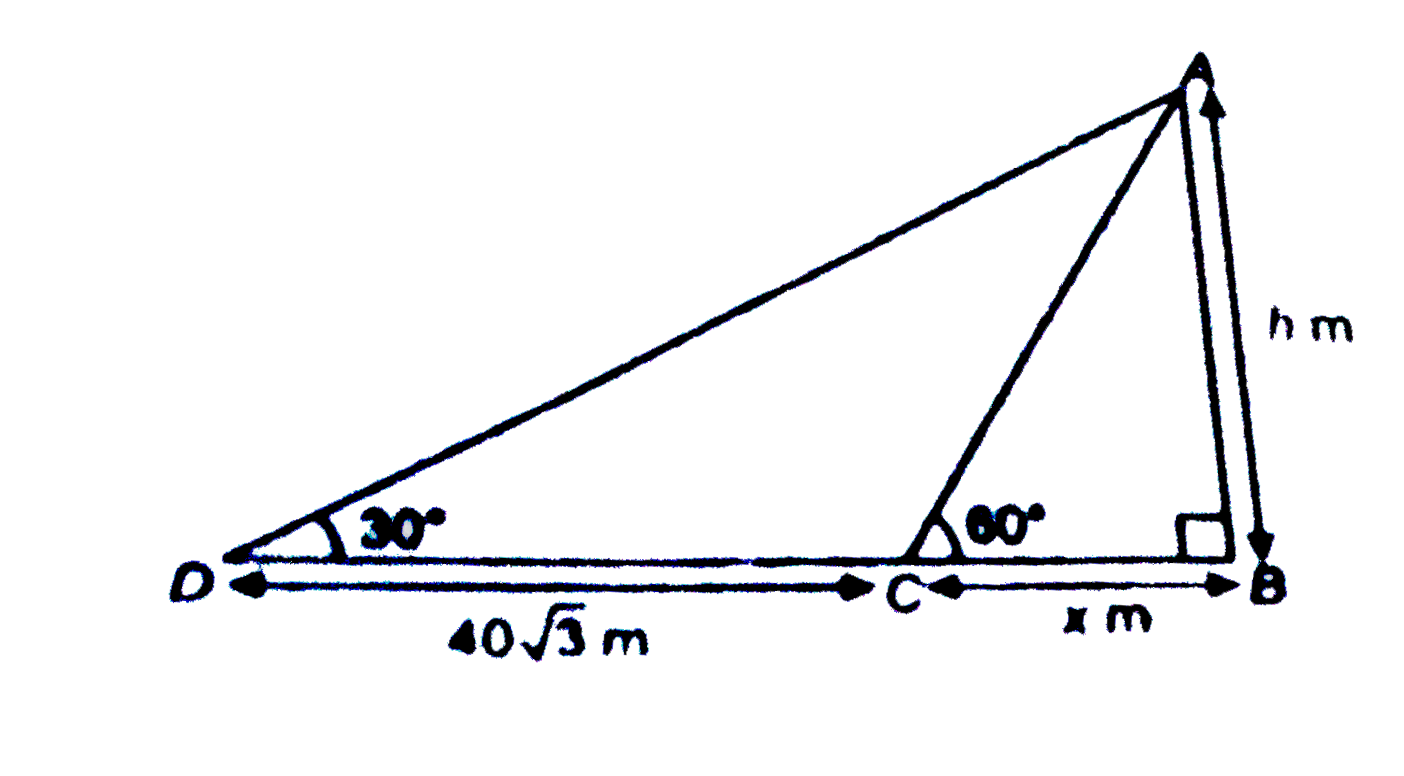
The angle of elevation of the top of a tower from a point on the ground is $30^{\circ}$ . After walking $40 \sqrt{3}$ m towards the tower, the angle of elevation becomes $60^{\circ}$ . Find the height of the tower.

Video Solution

Text Solution

Verified by Experts

Let AB be a tower of height 'h' metres. From points D and C on the ground, the angle of elevation of top A of the tower are $30^{\circ} and 60^{\circ}$ respectively.
Given that $C D = 40 \sqrt{3} m$
In $Δ A B C$
${tan 60}^{\circ} = \frac{A B}{B C} \Rightarrow \sqrt{3} = \frac{h}{x}$
$\Rightarrow x = \frac{h}{\sqrt{3}} ... (i)$
In $Δ A B D$
${tan 30}^{\circ} = \frac{A B}{B D} \Rightarrow \frac{1}{\sqrt{3}} = \frac{h}{40 \sqrt{3} + x}$
$\Rightarrow \sqrt{3} h = 40 \sqrt{3} + x \Rightarrow \sqrt{3} h = 40 \sqrt{3} + \frac{h}{\sqrt{3}}$
$\Rightarrow 3 h = 120 + h 2 h = 120$
$\Rightarrow h = 60$
$∴ Height of the tower = 60 m$

|

Updated on:21/07/2023

Class 10 MATHS SOME APPLICATIONS OF TRIGONOMETRY

Topper's Solved these Questions

Similar Questions

Knowledge Check

Question 1 - Select One
The angle of elevation of the top of a tower at a point G on the ground is $30^{\circ}$ . On walking 20 m towards the tower the angle of elevation becomes $60^{\circ}$ . The height of the tower is equal to :
A $10 / \sqrt{3} m$
B $20 \sqrt{3} m$
C $20 / \sqrt{3} m$
D $10 \sqrt{3} m$
Question 2 - Select One
The angle of elevation of the top of a tower at point on the ground is $30^{\circ}$ . If on walking 20 metres towards the tower, the angle of elevation become $60^{\circ}$ then the height of the tower is
A10 metres
B $\frac{10}{\sqrt{3}}$ metres
C $10 \sqrt{3}$ m
DNone of these
Question 3 - Select One
The angle of elevation of the top of a tower at a point on the ground is $30^{\circ}$ . If on walking 20 m toward the tower, the angle of elevation becomes $60^{\circ}$ , then the height of the tower is
A10 m
B $\frac{10}{\sqrt{3}} m$
C $10 \sqrt{3} m$
DNone of these

NAGEEN PRAKASHAN-SOME APPLICATIONS OF TRIGONOMETRY-Long Answer Questions

Home
Ask Doubt
Profile