Solve the following system of equations
bx + ay = 2ab and ax−by=a2−b2.
Given equations can be written as
bx + ay - 2ab = 0
and ax - by - a2+b2=0
By cross multiplication method, we have
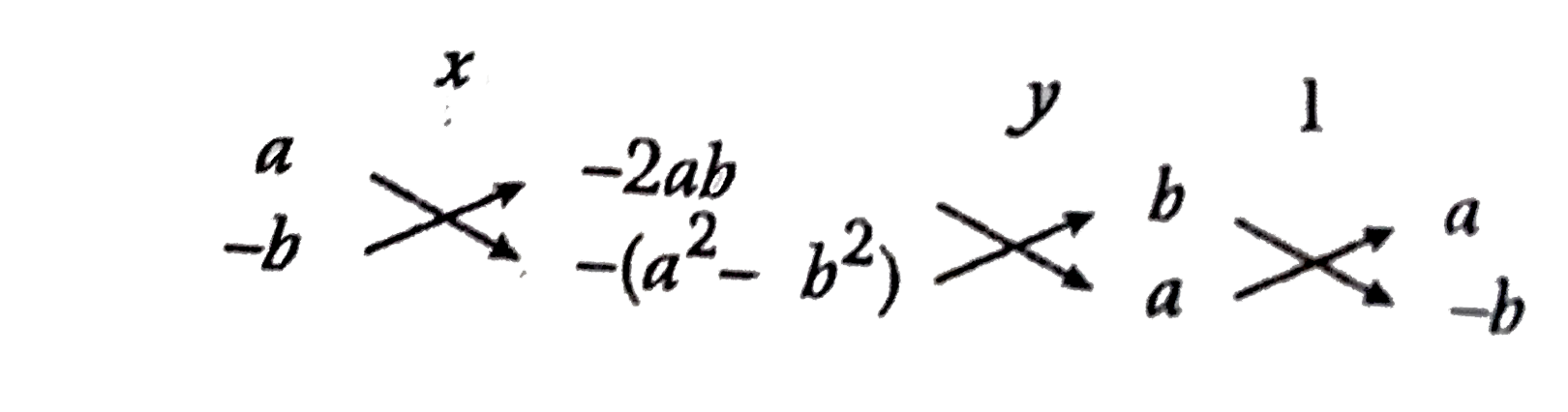
xa×[−(a2−b2)]−(−b)×(−2ab)=y(−2ab)×a−[−(a2−b2)]×b=1b×(−b)−a×a
⇒xa(−a2+b2−2ab2)=y−2a2b+a2b−b3=1−b2−a2
implies xa(−a2−b2)=y−a2b−b3=1−b2−a2
when xa(−a2−b2)=1−b2−a2
⇒x=−a(a2+b2)−1(b2+a2)orx=a
and y−a2b−b3=1−b2−a2
implies y=−b(a2+b2)−1(b2+a2)ory=b
Hence, x=ay=b} is the required solution.
Topper's Solved these Questions
- LINEAR EQUATIONS IN TWO VARIABLES BOOK - NAGEEN PRAKASHANCHAPTER - LINEAR EQUATIONS IN TWO VARIABLES EXERCISE - Exercise 3a
18 Videos
- LINEAR EQUATIONS IN TWO VARIABLES BOOK - NAGEEN PRAKASHANCHAPTER - LINEAR EQUATIONS IN TWO VARIABLES EXERCISE - Exercise 3b
30 Videos
- INTRODUCTION TO TRIGONOMETRYBOOK - NAGEEN PRAKASHANCHAPTER - INTRODUCTION TO TRIGONOMETRYEXERCISE - Revision Exercise Long Answer Questions
5 Videos
- POLYNOMIALSBOOK - NAGEEN PRAKASHANCHAPTER - POLYNOMIALSEXERCISE - Revision Exercise Long Answer Questions
4 Videos
Similar Questions
Solve the following system of equations: ax+by=c,x+ay=1+c
View SolutionSolve the following system of equations: x+y=a−b, ax−by=a2+b2
View SolutionSolve the following system of linear equations. :
(a−b)x+(a+b)y=a2−2ab−b2 ,
(a+b)(x+y)=a2+b2.
View SolutionSolve the following system of equations in xandy ax+by=1 bx+ay=(a+b)2a2+b2−1or,bx+ay=2aba2+b2
View SolutionSolve the following linear equations:
ax+by=c
bx+ay=1+c
View SolutionSolve the following
x+ay=b
ax−by=c
View SolutionSolve the following system of equations bxa−ayb+a+b=0 , bx−ay+2ab=0
View SolutionSolve the following simultaneous equations: ax+by=a−b;bx=ay+a+b
View SolutionSolve the following system of equations by method of cross-multiplication: ax+by=a2, bx+ay=b2
View SolutionSolve the following system of equations by method of cross-multiplication: ax+by=a−b, bx−ay=a+b
View Solution
