If √3tanθ=1 then find value of sin2θ−cos2θ
Video Solution
Text Solution
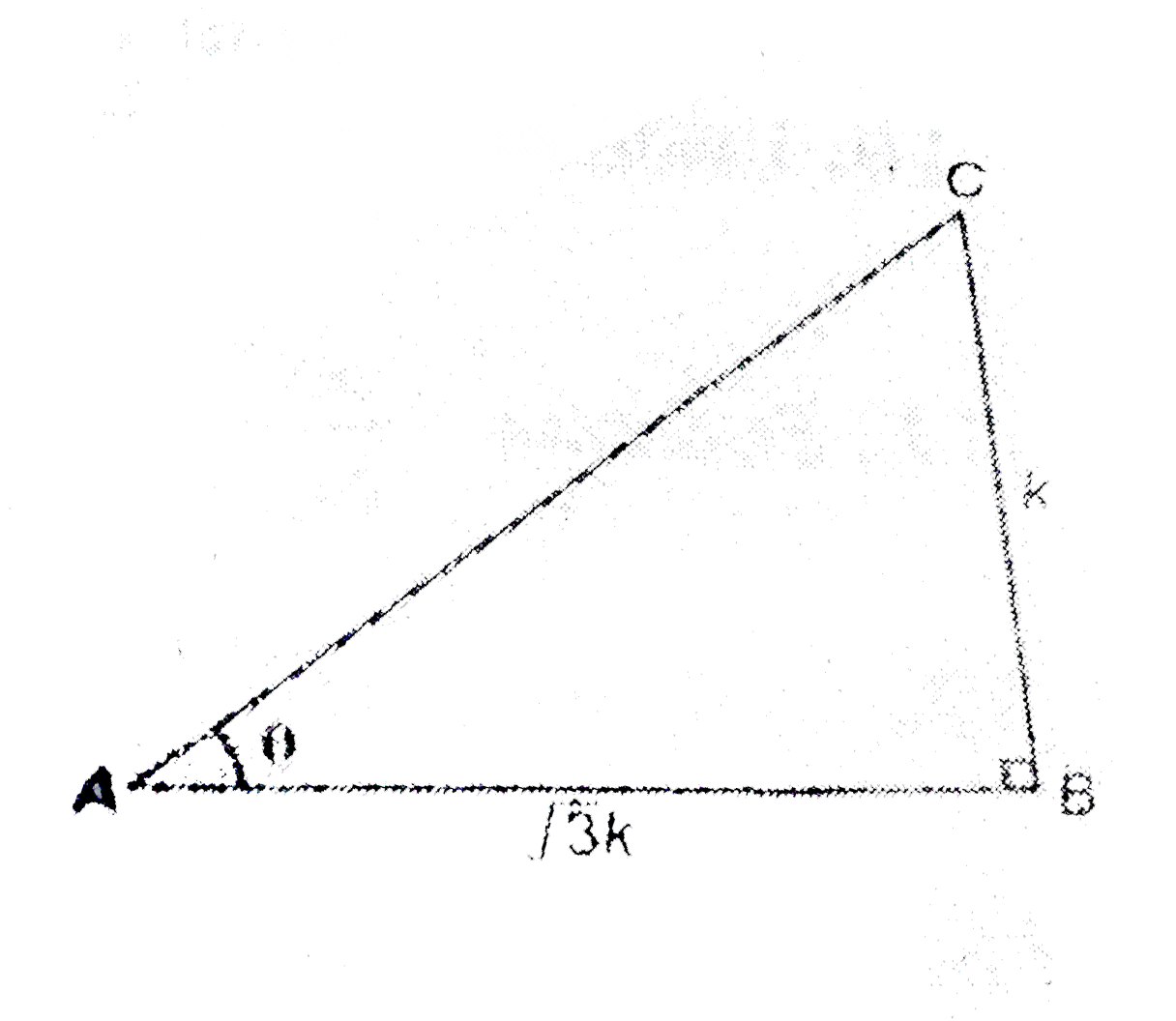
√3tanθ=1⇒tanθ=1√3
Construct ΔABC , right - angled at B such that
BC=k,AB=√3k
and <BAC=θ
In ΔABC,
From Pythagoras theorem
AC2=AB2+BC2=(√3k)2+(k)2=4k2
⇒AC=2k
∴sinθ=BCAC=k2k=12
and cosθ=ABAC=√3k2k=√32
Now , sin2θ−cos2θ=(12)2−(√32)2=14−34=−12
|
Updated on:21/07/2023
Topper's Solved these Questions
- BOOK - NAGEEN PRAKASHANCHAPTER - INTRODUCTION TO TRIGONOMETRYEXERCISE - Exercise 8a20videos
INTRODUCTION TO TRIGONOMETRY
- BOOK - NAGEEN PRAKASHANCHAPTER - INTRODUCTION TO TRIGONOMETRYEXERCISE - Exercise 8 B22videos
INTRODUCTION TO TRIGONOMETRY
- BOOK - NAGEEN PRAKASHANCHAPTER - INTRODUCTION TO TRIGONOMETRYEXERCISE - Revision Exercise Long Answer Questions5videos
INTRODUCTION TO TRIGONOMETRY
- BOOK - NAGEEN PRAKASHANCHAPTER - CONSTRUCTIONSEXERCISE - PROBLEMS FROM NCERT/ EXEMPLAR10videos
CONSTRUCTIONS
- BOOK - NAGEEN PRAKASHANCHAPTER - LINEAR EQUATIONS IN TWO VARIABLES EXERCISE - Revision Exercise Long Answer Questions8videos
LINEAR EQUATIONS IN TWO VARIABLES
Similar Questions
Knowledge Check
- Question 1 - Select One
If tanθ.tan2θ=1, then find the value of sin22θ+tan22θ.
A34B103C334D3 - Question 2 - Select One
If √5tanθ=5sinθ then what is the value of (sin2θ−cos2θ) ?
AA)3/5BB)1/5CC)4/5DD)2/5 - Question 3 - Select One
If tanθ=1, then the value of 8sinθ+5cosθsin3θ−2cos3θ+7cosθ is
A2B212C3D45
If tanθ=1√5 find the value of cosec2θ−sec2θ
View SolutionIf √3sinθ=cosθ, find the value of 3cos2θ+2cosθ3cosθ+2
View SolutionIf √3 sinθ=cosθ, find the value of sinθ tanθ (1+cotθ)sinθ+cosθ
View Solutionsinθ+cosθ=√3cosθ then find the value of cosθ−sinθ is
View SolutionIf 3cosθ=5sinθ, then find the value of 5sinθ−2sec3θ+2cosθ5sinθ+2sec3θ−2cosθ
View Solution

