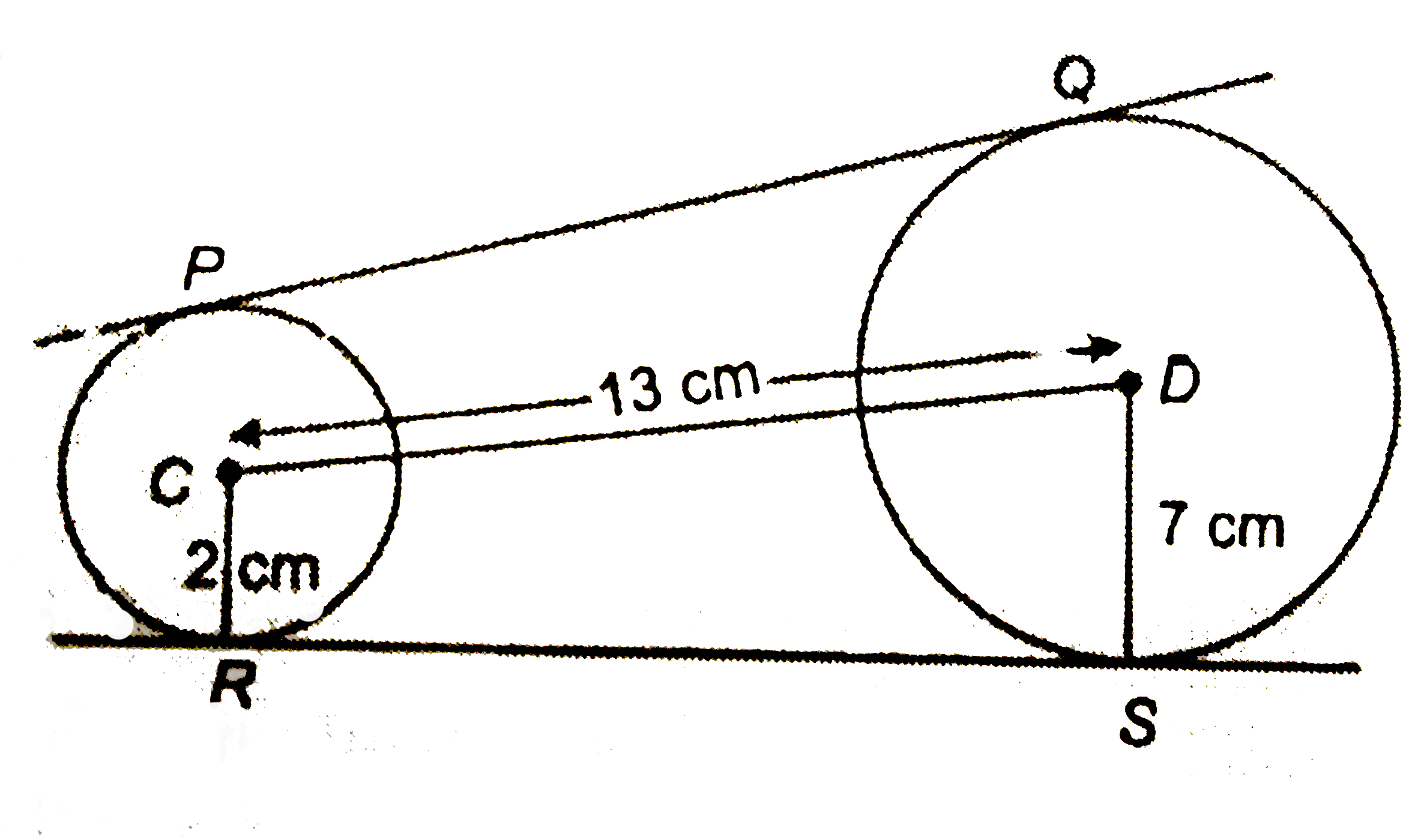
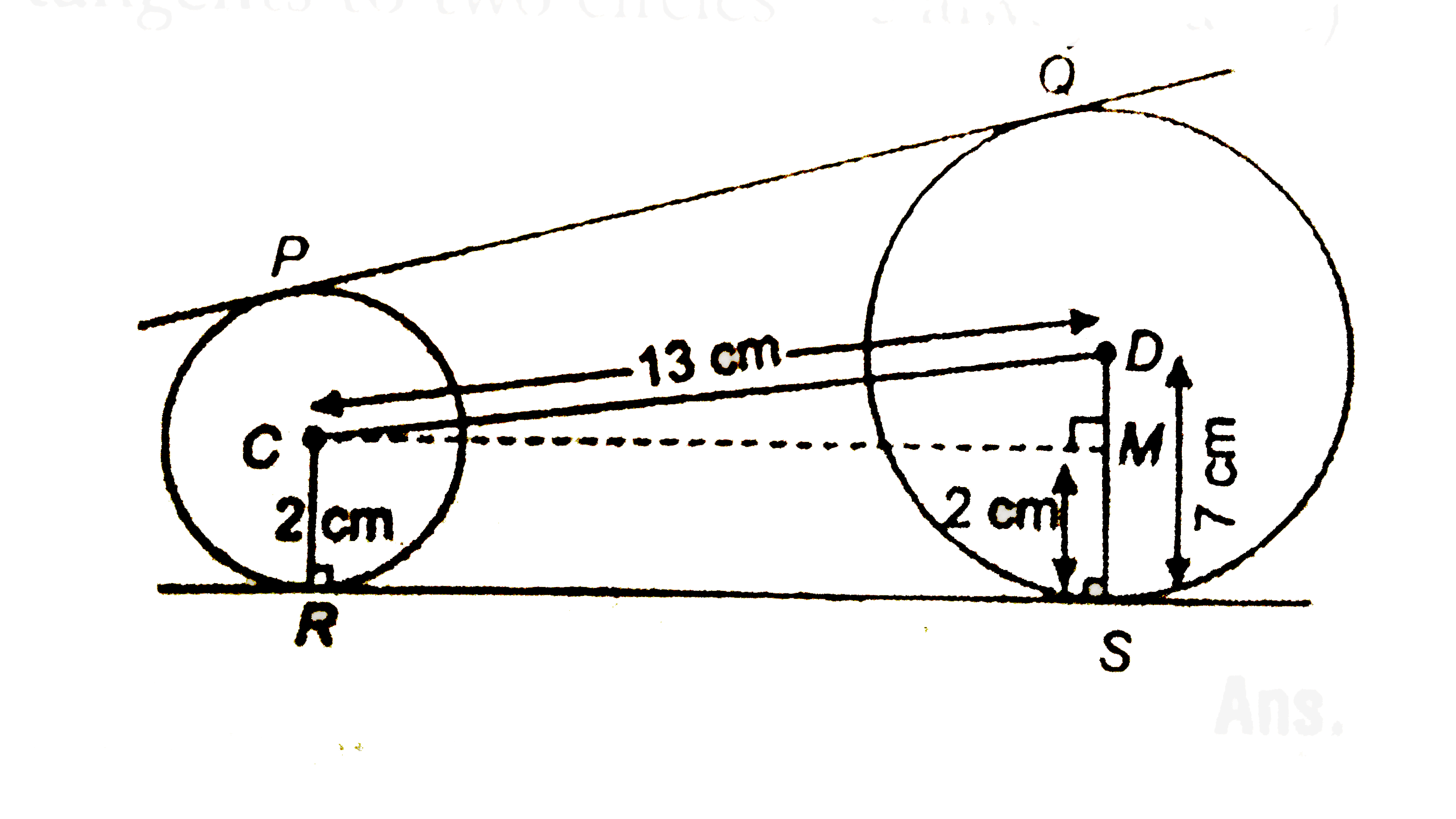
In the given diagram, PQ and RS are common tangents to the two circles with centres C and D. Find the length of PQ and hence area of trapexium RSDC.
Video Solution
Text Solution
Draw CM||RS so that □CMSRbecomes a rectangle, Now, we have CR=2 cm, DS=7 cm and CD=13 cm
∴ DM=DS−MS
=DS−CR
=7−2=5cm
In right ΔDMC, by Pythagoras theorem,
CM2=CD2−DM2
=(13)2−(5)2=(12)2
∴ CM=12cm
⇒ RS=12cm (∵opposite sides of rectangle are equal)
∴ PQ=12cm (∵length of common tangents to two circles are always same)
=12×h(sum of parallel sides)
=12×CM(CR+DS)
=12×12(2+7)=54cm2
|
Topper's Solved these Questions
- CIRCLESBOOK - NAGEEN PRAKASHANCHAPTER - CIRCLESEXERCISE - Problems From NCERT/exemplar
11 Videos
- CIRCLESBOOK - NAGEEN PRAKASHANCHAPTER - CIRCLESEXERCISE - Exercise
25 Videos
- ARITHMETIC PROGRESSIONBOOK - NAGEEN PRAKASHANCHAPTER - ARITHMETIC PROGRESSIONEXERCISE - Revision Exercise Long Answer Question
5 Videos
- CO-ORDINATE GEOMETRYBOOK - NAGEEN PRAKASHANCHAPTER - CO-ORDINATE GEOMETRYEXERCISE - Revision Exercise Short Answer Questions
9 Videos
Similar Questions
Knowledge Check
In the given figure , AB is a tangent to the circle with centre O and ∠BPQ=40∘ . Find PQ : AQ.
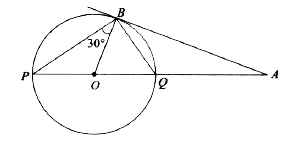 A1:2B1:3C2:1D3:1
A1:2B1:3C2:1D3:1If PQ and PR are two tangents to ta circle with centre O. if ∠QPR=46∘, then ∠QOR is equal to
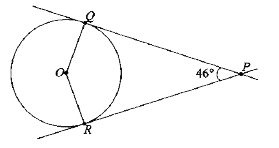 A67∘B46∘C44∘D134∘
A67∘B46∘C44∘D134∘Two circles of radii 8 cm and 2 cm respectively touch each other externally at the point A. PQ is the direct common tangent of these two circles of centres O1andO2 respectively. The length of PQ is equal to :
A4 cmB8 cmC2 cmD3 cm
In the given figure, PQ is tangent at a point R of the circle with centre O. If , find m∠PRS.
View SolutionIn figure, PQ and PR are two tangents to a circle with centre O. IF ∠QPR=46∘ , then ∠QOR equals

View SolutionIn fig. PQ is a tangent to length 6cm to the circle with centre O and ∠OQP=60∘ . Find OQ

View SolutionIn the give figure ,PQ and PR are tangents to the given circle such that PQ =5 cm and ∠QPR=60∘. The length of chord QR is
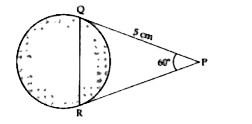
View SolutionTwo circles of radii 8 cm and 2 cm respectively touch each other externally at the point A. PQ is the direct common tangent of those two circles of centres O1 and O2 respectively. Then length of PQ is equal to
View Solution