Find the largest number that will divide 400 , 437 and 542 leaving 9, 12, 15 respectively .
We have to find a number , which divides the other number means → H.C.F.
It is given that the required number , when divides 400 , 437 and 542 leaving remainders 9 , 12 and 15 respectively . It means that if 400 is 9 less , 437 is 12 less and 542 is 15 less , then on division , gives no remainder (extra) .
∴400−9=391,437−12=425 and 542 - 15 = 527 are completely divisible by the required number .
First we will find the H.C.F. of 391 and 425 .

∴ 425=391×1+34
391=34×11+17
34=17×2+0
∴ H.C.F. (391, 425) = 17
Now , we will find the H.C.F. of 17 and 527.
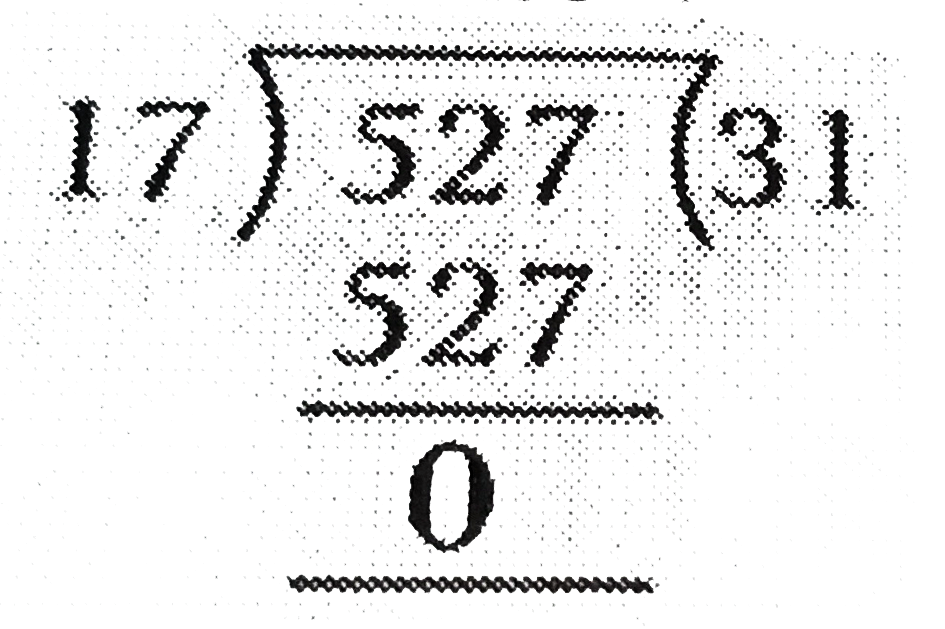
∴ 527=17×31+0
⇒ H.C.F. (17, 527) = 17
∴ Required number = 17
Related Playlists
- BOOK - NAGEEN PRAKASHANCHAPTER - REAL NUMBERSEXERCISE - Solved Example15videos
REAL NUMBERS
- BOOK - NAGEEN PRAKASHANCHAPTER - REAL NUMBERSEXERCISE - Problems From NCERT/ Exemplar11videos
REAL NUMBERS
- BOOK - NAGEEN PRAKASHANCHAPTER - QUADRATIC EQUATIONSEXERCISE - Revision Exercise Long Answer Questions6videos
QUADRATIC EQUATIONS
- BOOK - NAGEEN PRAKASHANCHAPTER - SOME APPLICATIONS OF TRIGONOMETRYEXERCISE - Long Answer Questions5videos
SOME APPLICATIONS OF TRIGONOMETRY
Similar Questions
Find the largest number that will divide 398, 436 and 542 leaving remainders 7, 11 and 15 respectively.
View SolutionFind the largest number that will divide 398, 436 and 542 leaving remainders 7,11 and 15 respectively.
View SolutionThe largest number that divides 64 and 72 and leave the remainders 12 and 7 respectively, is 17 (b) 13 (c) 14 (d) 18
View SolutionFind the largest number that divides 32 and 99 having leaving remainder 5 and 8 respectively.
View SolutionFind the largest number that divides 59 and 54 leaving remainders 3 and 5 respectively.
View SolutionFind the largest number which divides 129 and 545, leaving remainder 3 and 5 respectively.
View SolutionFind the largest number that divides 280 and 1248 leaving remainders 4 and 6 respectively.
View SolutionFind the largest number which divides 320 and 457 , leaving remainders 5 and 7 respectively .
View SolutionFind the largest number that divides 59 and 54 leaving remainders 3 and 5 respectively.
View SolutionFind the largest number which divides 630 and 940 leaving remainders 6 and 4 respectively
View Solution


