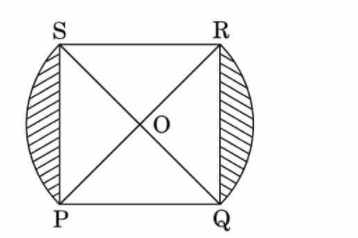
In Figure, two circular flower beds have been shown on two sides of a square lawn ABCD of side 56m. If the centre of each circular flower bed is the point of intersection of the diagonals of the square lawn, find the sum of the areas of the lawns and the flower beds.

Video Solution

Text Solution

Verified by Experts

We know that the diagonals of a square bisect each other perpendicularly
$∴ A n g \leq D O C = 90^{\circ}$
Also, diagonal BD = side $\sqrt{2} = 56 \sqrt{2} m$
$∴ O D = \frac{1}{2} \times B D = 28 \sqrt{2} m$
$∴$ Area of $Δ D O C = \frac{1}{2} \times 28 \sqrt{2} \times 28 \sqrt{2} = {(28)}^{2} m^{2}$
Area of sector ODCO $= π {(O D)}^{2} \times \frac{θ}{360^{\circ}}$
$= π {(28 \sqrt{2})}^{2} \times \frac{90^{\circ}}{360^{\circ}} = \frac{11 \times 28 \times 28}{7} m^{2}$
$= 1232 m^{2}$
$∴$ Area of 1 flower bed = Area of sector - Area of $Δ$
$∴$ Area of 2 flower beds = $2 \times 448 = 896 m^{2}$
Area of square lawn $= {(56)}^{2} = 3136 m^{2}$
$∴$ Required area $= 896 + 3136 = 4032 m^{2}$

|

Updated on:21/07/2023

Class 10 MATHS AREAS RELATED TO CIRCLES

Topper's Solved these Questions

Similar Questions

NAGEEN PRAKASHAN-AREA RELATED TO CIRCLES-Problems From NCERT /exemplar

Home
Ask Doubt
Profile