Consider a square ABCD of side 12 and let M, N be the midpoints of AB, CD respectively. Take a point P on MN and let AP=r, PC=s. Then the area of the triangle whose sides are r, s, 12 is-
72
36
rs2
rs7
The correct Answer is:B
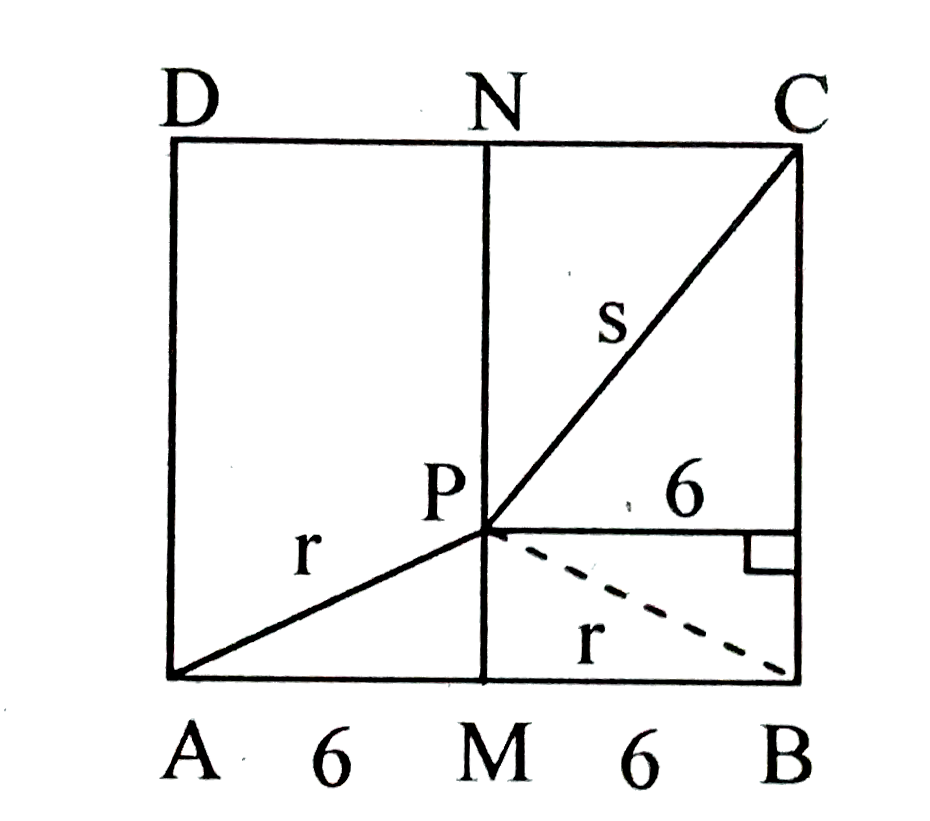
PA=r, PC = s
So PB = r
Triangle with sides r, s & 12 is ΔPCB

area=12base×height=12×6×12=36
Topper's Solved these Questions
Similar Questions
Knowledge Check
If ABCD be a rectangle and P, Q, R, S be the mid-points of AB, BC, CD and DA respectively, then the area of the quadrilateral PQRS is equal to
A13 are (ABCD)B34 area (ABCD)C12 area (ABCD)Darea (ABCD)OPQR is a square with M and N as the middle points of the sides PQ and QR, respectively. The ratio of the areas of the square and the triangle OMN is
A4:1B2:1C8:3D4:3Let WXYZ be a square. Let P, Q, R, be the midpoints of WX, XY and ZW respectively and K, L be the midpoints of PQ and PR respectively. What is the value of
Area of triangle PKLArea of square WXYZ=?A132B116C18D164
Find the area of a triangle ABC whose sides are 9m ,12m and 15m respectively.
View SolutionLet ABCD be a rectangle. Let P, Q, R, S be the mid-points of sides AB, BC, CD, DA respectively. Then the quadrilateral PQRS is a
View SolutionLet P, Q, R be the mid-points of sides AB, BC, CA respectively of a triangle ABC. If the area of the triangle ABC is 5 square units, then the area of the triangle PQR is
View SolutionIf a,b∈N, PQRS is a square and P, Q, R, S are mid points of AB, AD, CD, BC respectively then a+b is
View SolutionABC is an equilateral triangle. P,Q and R are the midpoints of sides AB, BC and CA respectively. If the length of the side of the triangle ABC is 8 cm, then the area of △PQR is:
ABC एक समबाहु त्रिभुज है | P, Q और R क्रमशः भुजाओं AB, BC तथा CA के मध्य बिंदु हैं | यदि त्रिभुज ABC की भुजा की लंबाई 8 सेमी है, तो त्रिभुज PQR का क्षेत्रफल कितना होगा ?
View Solution
