A projectile is thrown from a point on ground with an initial speed u and at anelevatio θ to the horizontal. Find the change in momentum of the particle, when it reaches the top most point of its trajectory.
0
mu
mucosθ
musinθ
The correct Answer is:D
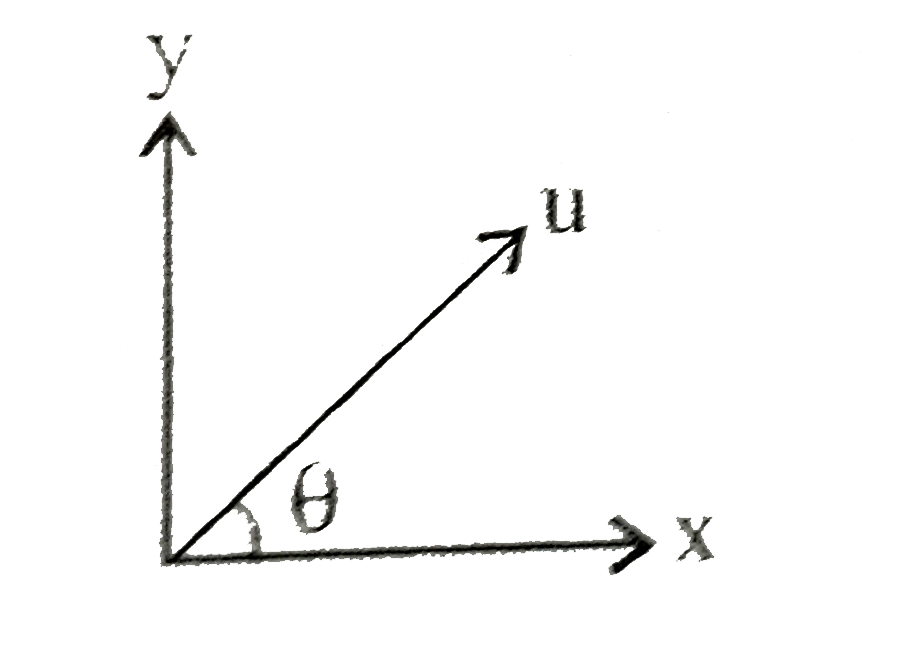
→P1=mucosθˆi+musinθˆj
(at height point) →Pt=mucosθˆi
Δ→P=→Pt−→Pi=−musinθˆj
Topper's Solved these Questions
- TEST PAPERSBook:BANSALChapter:TEST PAPERSExercise:PHYSICS PART (A)
Explore 32 Videos
- TEST PAPERSBook:BANSALChapter:TEST PAPERSExercise:PHYSICS PART (B)
Explore 3 Videos
- TEST PAPERSBook:BANSALChapter:TEST PAPERSExercise:PHYSICS PART- C
Explore 4 Videos
- SEMICONDUCTORSBook:BANSALChapter:SEMICONDUCTORSExercise:CBSE Question
Explore 32 Videos
Similar Questions
A particle is projected from the ground with an initial speed v at an angle θ with horizontal. The average velocity of the particle between its point of projection and highest point of trajectory is [EAM2013]
View SolutionA particle of mass m is projected with velocity v at an angle θ with the horizontal. Find its angular momentum about the point of projection when it is at the highest point of its trajectory.
View Solution
Knowledge Check
A particle is fired from a point on the ground with speed u making an angle θ with the horizontal.Then
Athe radius of curvature of the projectile at the highest point is u2cos2θgBthe radius of curvature of the projectile at the highest point is u2sin2θgCat the point of projection magnitude of tangential acceleration is gsinθDat the point of projection magnitude of tangential acceleration is gcosθA particle is projected from the ground with an initial speed of v at an angle θ with horizontal. The average velocity of the particle between its point of projection and highest point of trajectroy is :
Av2√1+2cos2θBv2√1+2cos2θCv2√1+3cos2θDvcosθA projectile of mass m is launched with an initial velocity →vi making an angle θ with the horizontal as shown in figure. The projectile momentum of the particle about the origin when it is at the highest point of its trajectory is.
 .A−m3isinθ2cosθ2gˆkBm3isinθ2cosθ2gˆkC−m3isinθ2cosθgˆkD2m3isinθ2cosθgˆk
.A−m3isinθ2cosθ2gˆkBm3isinθ2cosθ2gˆkC−m3isinθ2cosθgˆkD2m3isinθ2cosθgˆk
A particle of mass m is projected with a speed u at an angle θ with the horizontal. Find angular momentum of particle after time t about point of projection.
View SolutionA particle of mass m is thrown with speed v0 at angle 30∘ with horizontal. Find the angular momentum about the point of projection when the particle is at the highest point of its trajectory.
View SolutionA body of mass m is projected with a velocity u at an angle θ with the horizontal. The angular momentum of the body, about the point of projection, when it at highest point on its trajectory is
View SolutionA particle of mass m is projected with a velocity μ at an angle of θ with horizontal.The angular momentum of the particle about the highest point of its trajectory is equal to :
View SolutionA projectile is projected with linear momentum p making angle θ with the horizontal. The change in momentum of the projectile on returning to the ground will be-
View Solution

