Show that pressure of a fixed amount of a ideal gas is a state function $V = \frac{n R T}{p}$

Video Solution

Text Solution

Verified by Experts

${(\frac{\partial V}{\partial T})}_{p} = \frac{n R}{P}$
$\frac{\partial}{\partial P} {[{(\frac{\partial V}{\partial T})}_{p}]}_{T} = \frac{n R}{P^{2}} \Rightarrow {(\frac{\partial V}{\partial p})}_{T} = \frac{n R T}{P^{2}}$
$\frac{\partial}{\partial T} {[{(\frac{\partial V}{\partial T})}_{p}]}_{T} = \frac{- n R}{P^{2}}$

|

Updated on:21/07/2023

Class 12 CHEMISTRY THERMODYNAMICS

Topper's Solved these Questions

Similar Questions

Knowledge Check

Question 1 - Select One
Assertion: The pressure of a fixed amount of an ideal gas is proportional to its temperature.
Reason: The Frequency of collisions and their impact both increase in proportion of the square root of temperature.
AIf both ( $A$ ) and ( $R$ ) are correct and ( $R$ ) is the correct explanation of ( $A$ ).
BIf both ( $A$ ) and ( $R$ ) are correct, but ( $R$ ) is not the correct explanation of ( $A$ ).
CIf ( $A$ ) is correct, but ( $R$ ) is incorrect.
DIf ( $A$ ) is incorrect, but ( $R$ ) is correct.
Question 2 - Select One or More
Assertion: The pressure of a fixed amount of an ideal gas is proportional to its temperature.
Reason: Frequency of collisions and their impact both increase in proportion of the square root of temperature.
AIf both ( $A$ ) and ( $R$ ) are correct and ( $R$ ) is the correct explanation of ( $A$ ).
BIf both ( $A$ ) and ( $R$ ) are correct, but ( $R$ ) is not the correct explanation of ( $A$ ).
CIf ( $A$ ) is correct, but ( $R$ ) is incorrect.
DIf ( $A$ ) is incorrect, but ( $R$ ) is correct.
Question 3 - Select One
For fixed amount of an ideal gas taken at constnat temperature V vs $\frac{1}{p^{2}}$ is :
A
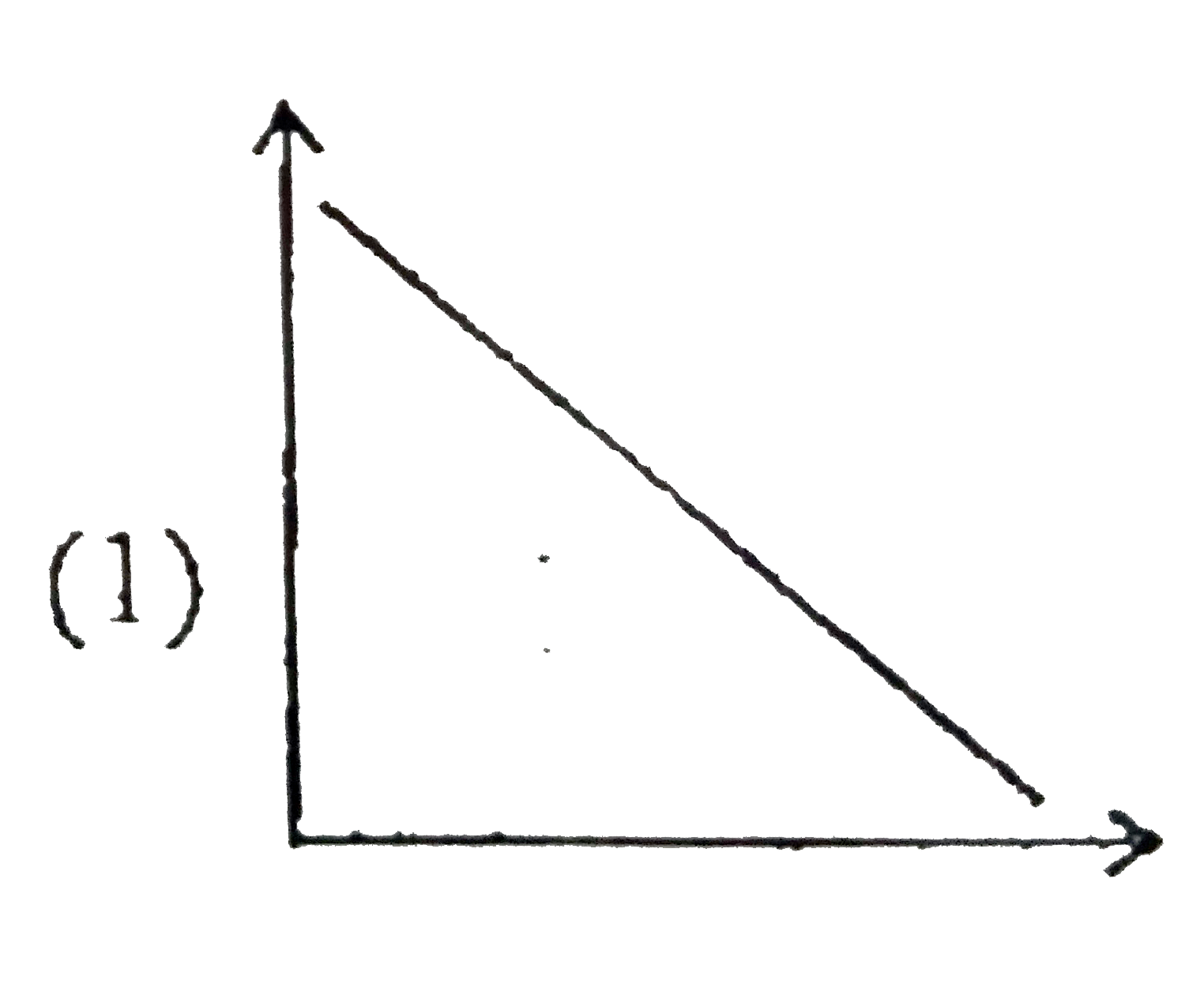B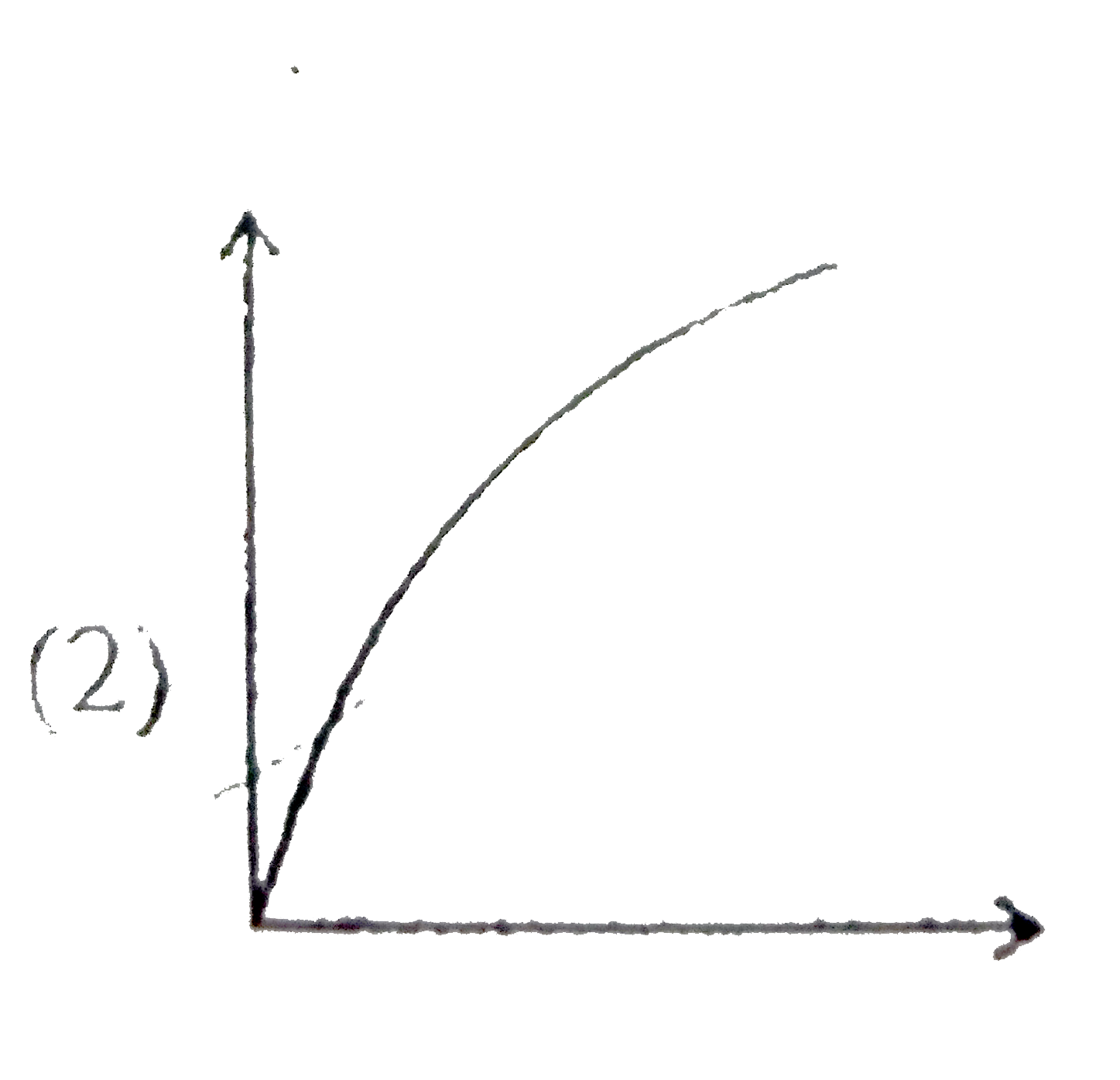
CE01_218_O03.png" width="30%">
DE01_218_O04.png" width="30%">

BANSAL-THERMODYNAMICS-Exercise 3

Home
Ask Doubt
Profile