To determine the half life of a radioactive element , a student plote a graph of in ∣∣∣dN(t)dt∣∣∣versust,Here∣∣∣dN(t)dt∣∣∣ is the rate of radioatuion decay at time t , if the number of radoactive nuclei of this element decreases by a factor of p after 4.16 year the value of p is
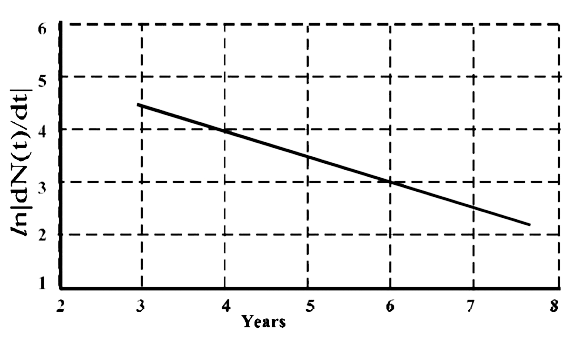
The correct Answer is:8
∣∣∣dNdt∣∣∣=λN0e−λt∴ln∣∣∣dNdt∣∣∣=ln(N0λ)−λt
∴ln∣∣∣dNdt∣∣∣=ln(N0λ)−λt⇒−λ= slope =−12year−1
⇒λ=12yr−1
∴t1/2=0.693λ=1.386 given time is 3 times of t1/2
∴ value of p is 8.
Topper's Solved these Questions
- BOOK - ALLENCHAPTER - SIMPLE HARMONIC MOTIONEXERCISE - Solved Example3videos
SIMPLE HARMONIC MOTION
- BOOK - ALLENCHAPTER - SIMPLE HARMONIC MOTIONEXERCISE - X Rays : Solved Example2videos
SIMPLE HARMONIC MOTION
- BOOK - ALLENCHAPTER - SIMPLE HARMONIC MOTIONEXERCISE - Paragraph3videos
SIMPLE HARMONIC MOTION
- BOOK - ALLENCHAPTER - RACEEXERCISE - Basic Maths (Wave Motion & Dopplers Effect) (Stationary waves & doppler effect, beats)25videos
RACE
- BOOK - ALLENCHAPTER - TEST PAPEREXERCISE - PHYSICS4videos
TEST PAPER
Similar Questions
To determine the half life of a radioactive element , a student plot a graph of in ∣∣∣dN(t)dt∣∣∣ versus t , Here ∣∣∣dN(t)dt∣∣∣ is the rate of radiation decay at time t , if the number of radioactive nuclei of this element decreases by a factor of p after 4.16year the value of p is
 View Solution
View SolutionDraw a graph showing the variation of decay rate (−dNdt) with number (N) of radioactive nuclei.
View Solution
Knowledge Check
- Question 1 - Select One
The graph between number of decayed atoms N' of a radioactive element and time t is.
A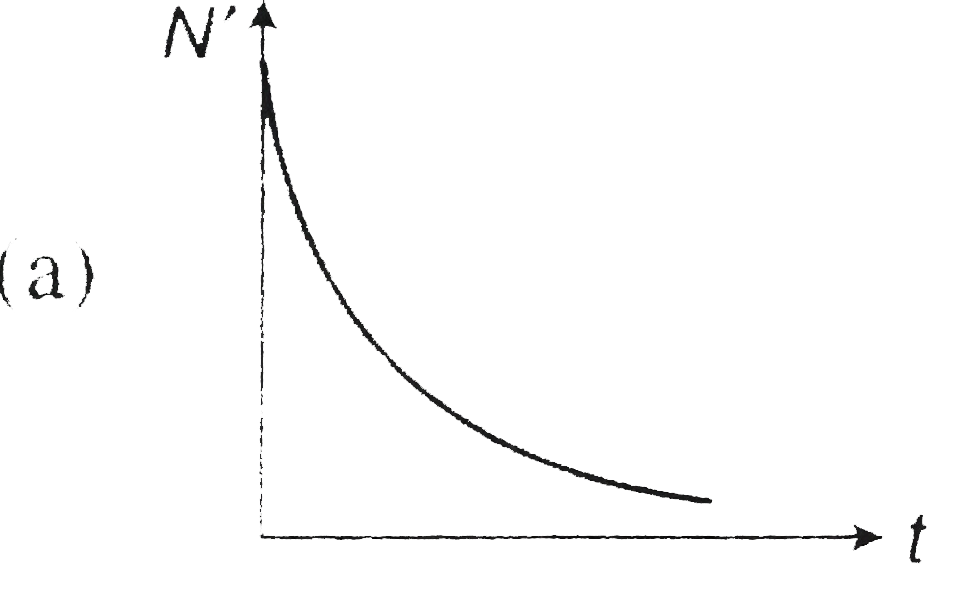 .B
.B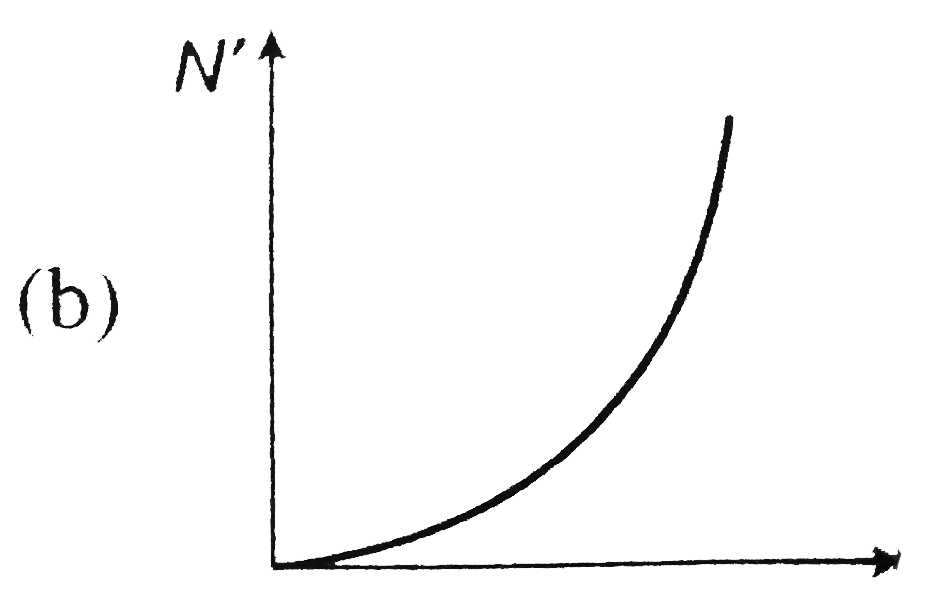 .C
.C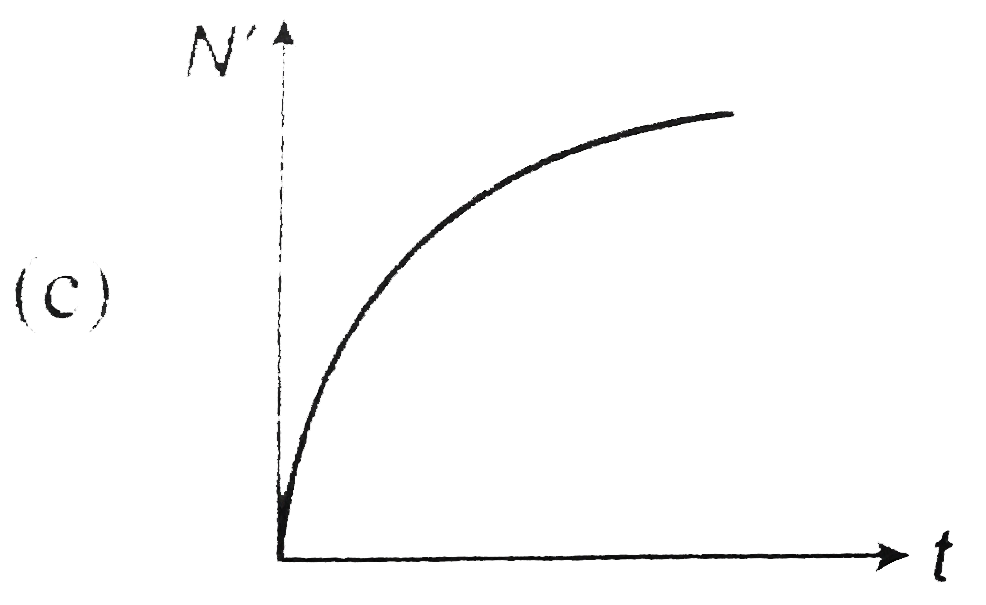 .D
.D .
. - Question 2 - Select One
The half-life period t1/2 of a radioactive element is N years. The period of its complete decays is
AN2 yearsB2N yearsC12N2 yearsDInfinity - Question 3 - Select One
If −(dNdt)o is the initial activity and −(dNdt) is the activity at time t in a radioactive disintegration then :
A−(dNdt)o=−(dNdt)e−ktB−(dNdt)o=(dNdt)oe−ktC−(dNdt)o=−(dNdt)oe−ktD−(dNdt)o=(dNdt)oe−kt
A radioactive sample decays to form a stable nuclide. A graph showing variation of rate of disintegration (dNdt) of radioactive sample with time (t) is
View SolutionNuclei of a radioactive element 'A' are being produced at a constant rate α the element has a decay constant λ At time t=0 there are N0 nuclei of the element
The number of nuclei of A at time 't' isView SolutionNuclei of a radioactive element A are being produced at a constant rate α. The element has a decay constant λ . At time t=0, there are N0 nuclei of the element . The number N of nuclei of A at time t is
View SolutionNuclei of a radioactive element 'A' are being produced at a constant rate, α . The element has a decay constant, λ. At time, t = 0, there are N0 nuclei of the element.
If α=2N0λ the number of nuclei of A after one half life of A becomesView SolutionThe half life of a radioactive substance is 20 minutes. The approximate time interval (t2–t1) between the time t2 when 34 of it has decayed and time t1 when 14 of it had decayed is
View Solution

