At time t=0N1 nuclei of decay constant λ1&N2 nuclei of decay constant λ2 are mixed. The decay rate of the mixture at time 't' is:
N1N2e(λ1+λ2)t
+(N1N2)e−(λ1−λ2)t
+(N2λ1eλ1t+N2λ2e−λ2t)
+N1λ1N2λ2e−(λ1+λ2)t
The correct Answer is:C
dNdt=λ1N1+λ2N2⇒λ1N10e−λ1t+λ2N20e−λ2t
Topper's Solved these Questions
- SIMPLE HARMONIC MOTIONBOOK - ALLENCHAPTER - SIMPLE HARMONIC MOTIONEXERCISE - Exercise - 29
2 Videos
- SIMPLE HARMONIC MOTIONBOOK - ALLENCHAPTER - SIMPLE HARMONIC MOTIONEXERCISE - Exercise - 30
2 Videos
- SIMPLE HARMONIC MOTIONBOOK - ALLENCHAPTER - SIMPLE HARMONIC MOTIONEXERCISE - Exercise - 57
1 Videos
- RACEBOOK - ALLENCHAPTER - RACEEXERCISE - Basic Maths (Wave Motion & Dopplers Effect) (Stationary waves & doppler effect, beats)
25 Videos
- TEST PAPERBOOK - ALLENCHAPTER - TEST PAPEREXERCISE - PHYSICS
4 Videos
Similar Questions
The decay constant (λ) for radioactive decay is independent of
View SolutionA radionuclide A1 with decay constant λ1 transforms into a radionuclide A2 with decay constant λ2. Assuming that at the initial moment the preparation contained only the radionuclide A1, find:
(a) the equation describing accumulation of the radionuclide A2 with time,
(b) the time interval after which the activity value.
View Solution
Knowledge Check
Uranium .23892U is an ustable nucleus. It decays to Thorium .23892Th, which is again an unstable nucleus which further decays to .23491Pa. Let .23892U be called A of decay constant λ1 and .23490Th is called as B of decay constant λ2 and stable nuclei .23491Pa be called as C. Here A is called parent nucleus and B is called daughter nucleus of A. Any two adjacent nuclei may be consider parent or daughter nuclei A,B and C respectively at time 't'.
Then we can write Aλ1−−→Bλ2−−→C
Rate of disintergration of A=dN1dt=λ1N1
Rate of disintergration of B=dN2dt=λ1N1−λ2N2
Rate of formation of nuclei C is equal to
dN3dt=λ2N2
If at t=0, there are N0 number of nuclei of A where as nuclei B and C are absent in the sample Answer the following questions ltbgt Numeber of the nuclei of nuclei C at time t isAN0[1+λ1λ2−λ1e−λ2t−λ2λ2−λ1e−λ1t]BN0[λ1λ2−λ1e−λ2t−λ2λ2−λ1e−λ1t]CN0λ1λ2−λ1(e−λ2t−e−λ1t)DN0[λ1λ2−λ1e−λ2t−λ2λ2−λ1e−λ1t−1]Uranium .23892U is an ustable nucleus. It decays to Thorium .23892Th, which is again an unstable nucleus which further decays to .23491Pa. Let .23892U be called A of decay constant λ1 and .23490Th is called as B of decay constant λ2 and stable nuclei .23491Pa be called as C. Here A is called parent nucleus and B is called daughter nucleus of A. Any two adjacent nuclei may be consider parent or daughter nuclei A,B and C respectively at time 't'.
Then we can write Aλ1−−→Bλ2−−→C
Rate of disintergration of A=dN1dt=λ1N1
Rate of disintergration of B=dN2dt=λ1N1−λ2N2
Rate of formation of nuclei C is equal to
dN3dt=λ2N2
If at t=0, there are N0 number of nuclei of A where as nuclei B and C are absent in the sample Answer the following questions
Number of nuclei of B at any time t isAN0λ1λ2−λ1(eλ1t−eλ2t)BN0λ1λ2−λ1(e−λ1t−e−λ2t)CN0λ1λ2−λ1(e−λ1t−e−λ2t)DN0λ2λ2−λ1(e−λ1t+e−λ2t)Uranium .23892U is an ustable nucleus. It decays to Thorium .23892Th, which is again an unstable nucleus which further decays to .23491Pa. Let .23892U be called A of decay constant λ1 and .23490Th is called as B of decay constant λ2 and stable nuclei .23491Pa be called as C. Here A is called parent nucleus and B is called daughter nucleus of A. Any two adjacent nuclei may be consider parent or daughter nuclei A,B and C respectively at time 't'.
Then we can write Aλ1−−→Bλ2−−→C
Rate of disintergration of A=dN1dt=λ1N1
Rate of disintergration of B=dN2dt=λ1N1−λ2N2
Rate of formation of nuclei C is equal to
dN3dt=λ2N2
If at t=0, there are N0 number of nuclei of A where as nuclei B and C are absent in the sample Answer the following questions
The graph N1,N2 and N3 with time can be best represent byA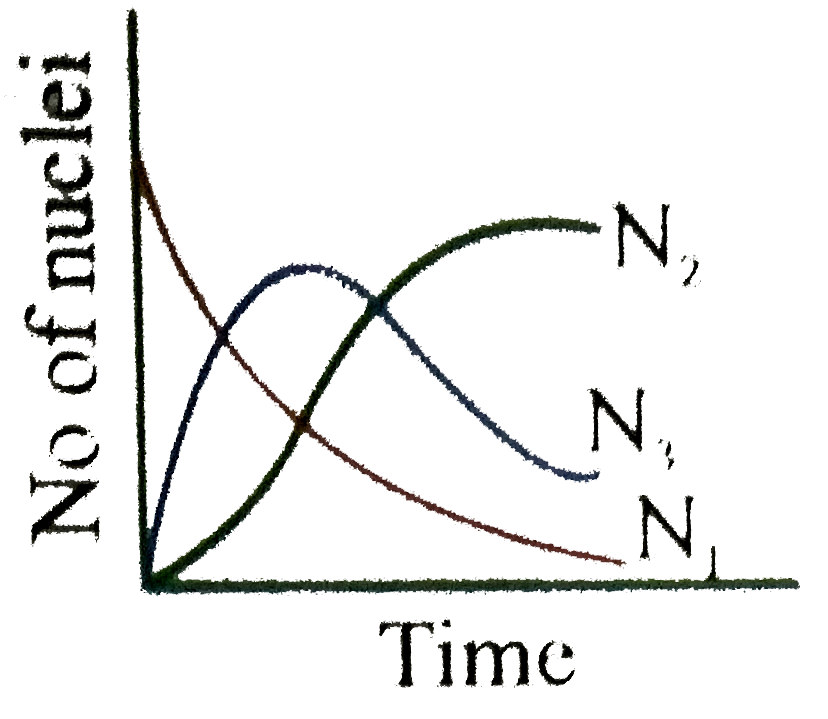 B
B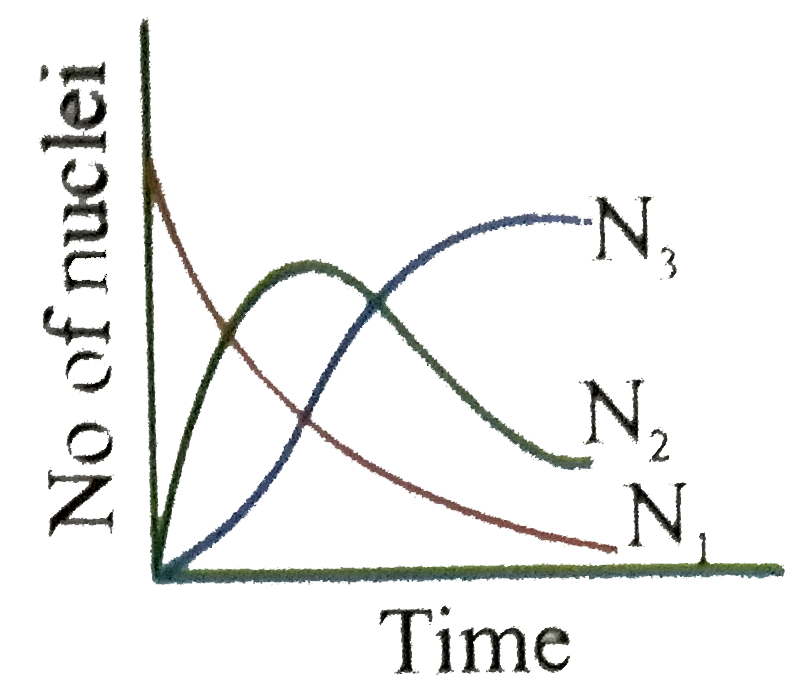 C
C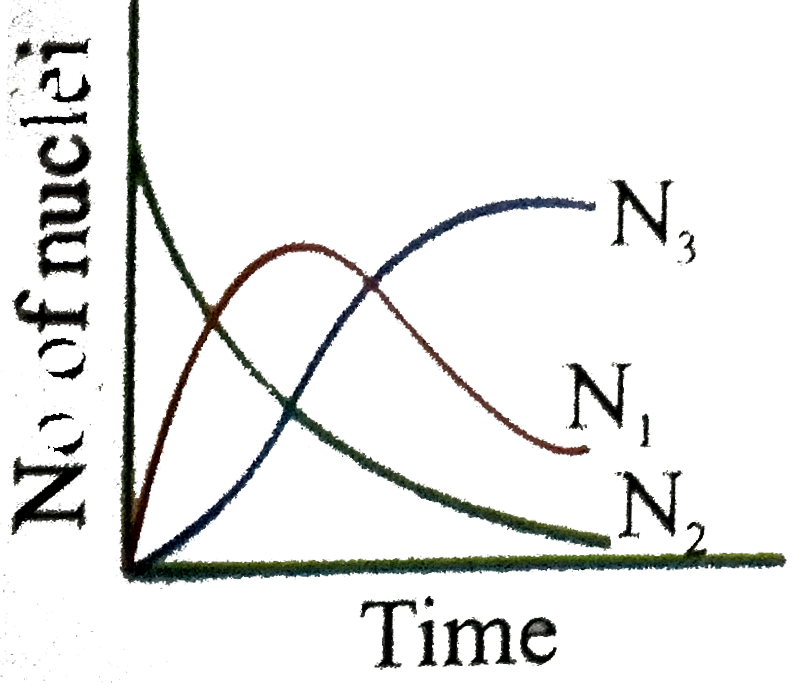 D
D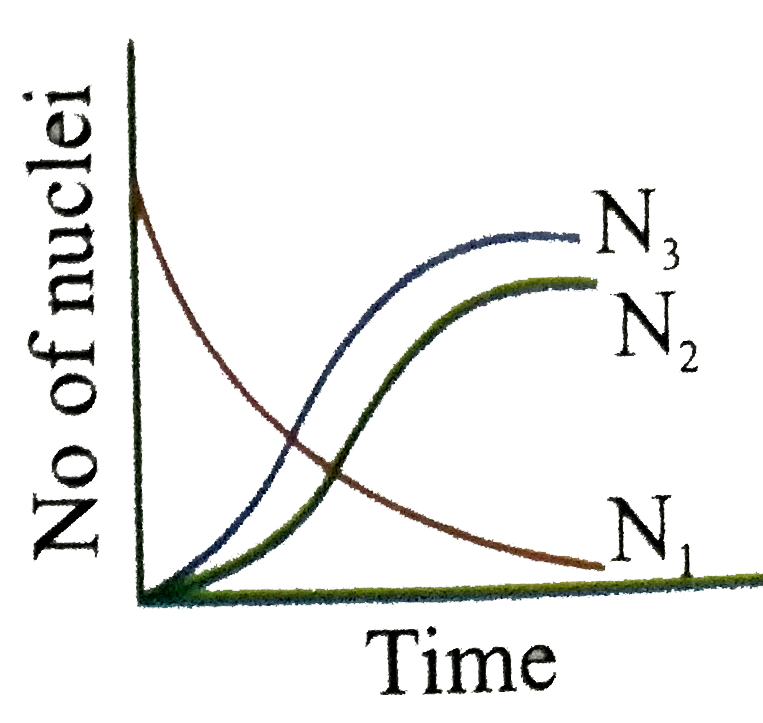
A radioactive substance A having N0 active nuclei at t=0, decays to another radioactive substance B with decay constant λ1. B further decays to a stable substance C with decay constant λ2. (a) Find the number of nuclei of A,B and C time t. (b) What should be the answer of part (a) if λ1>>λ2 and λ1<<λ2
View SolutionA radioactive element A of decay constant λA decays into another radioactive element B of decay constant λB. Initially the number of active nuclei of A was N0 and B was absent in the sample. The maximum number of active nuclei of B is found at t=2. In 2/λA. The maximum number of active nuclei of B is
View SolutionNucleus A decays to B with decay constant λ1 and B decays to C with decay constant λ2. Initially at t=0 number of nuclei of A and B are 2N0 and N0 respectively. At t=to, no. of nuclei of B is 3N02 and nuclei of B stop changing. Find t0?
View SolutionNucleus A decays into B with a decay constant λ1 and B further decays into C with a decay constant λ2 . Initially, at t = 0, the number of nuclei of A and B were 3N0 and N0 respectively. If at t = t0 number of nuclei of B becomes constant and equal to 2N0, then
View SolutionA radioacitve nucleus is being produced at a constant rate α per second. Its decay constant is λ. If N0 are the number of nuclei at time t=0, then maximum number of nuceli possible are .
View Solution
