An object of mass m is moving in unifrom circular motion in xy-plane. The circle has radius R and object is moving clockwise around the circle with speed v. The motion is projected onto the x-axis where it appears as simple harmonic motion accoding to x(t)=Rcos(ωt+ϕ). The motion starts from pointof coordinates
(0,R).
In this projection ϕ is-
π/2
π
3π/2
0
The correct Answer is:C
At t=0,x=0,v=v0=ωR
so cos(ωt+ϕ)=0 & −sin(ωt+ϕ)=+1⇒ϕ=3π2
Topper's Solved these Questions
- SIMPLE HARMONIC MOTIONBook:ALLENChapter:SIMPLE HARMONIC MOTIONExercise:Comprehension Base Questions (5)
Explore 3 Videos
- SIMPLE HARMONIC MOTIONBook:ALLENChapter:SIMPLE HARMONIC MOTIONExercise:Exercise-04 [A]
Explore 20 Videos
- SIMPLE HARMONIC MOTIONBook:ALLENChapter:SIMPLE HARMONIC MOTIONExercise:Comprehension Base Questions (3)
Explore 2 Videos
- RACEBook:ALLENChapter:RACEExercise:Basic Maths (Wave Motion & Dopplers Effect) (Stationary waves & doppler effect, beats)
Explore 25 Videos
- TEST PAPERBook:ALLENChapter:TEST PAPERExercise:PHYSICS
Explore 4 Videos
Similar Questions
Knowledge Check
An object of mass m is moving in unifrom circular motion in xy-plane. The circle has radius R and object is moving clockwise around the circle with speed v. The motion is projected onto the x-axis where it appears as simple harmonic motion accoding to x(t)=Rcos(ωt+ϕ). The motion starts from pointof coordinates
(0,R)
In this projection ω is -Av/RBm2/RCR/vDNone of theseFor a particle in uniform circular motion , the acceleration →a at a point p(R,θ) on the circle of radiu R is ( Here θ is measured from the x−aξs )
A−v2Rcosθˆi+v2RsinθˆjB−v2Rsinθˆi+v2RcosθˆjC−v2Rcosθˆi−v2RsinθˆjD−v2Rˆi+v2RˆjFor a particle in uniform circular motion the acceleration →a at a point P(R,θ) on the circle of radius R is : ( here θ is measured from the x- axis )
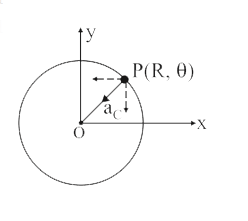 A−v2Rcosθˆi+v2RsinθˆjB−v2Rsinθˆi+v2RcosθˆjC−v2Rcosθhai−v2RsinθˆjDv2Rˆi+v2Rˆj
A−v2Rcosθˆi+v2RsinθˆjB−v2Rsinθˆi+v2RcosθˆjC−v2Rcosθhai−v2RsinθˆjDv2Rˆi+v2Rˆj
If an object of mass m moves in uniform circular motion, a formce F acts on it, whose direction is always towards the centre of the circular path. If F depends on m, speed v of the object and radius r of the circular path, find an expression for F.
View SolutionFor a particle in uniform circular motion, the acceleration →a at a point P(R,θ) on the circle of radius R (Here is measured from the x-axis) is
View SolutionA particle moves on the X-axis according to the equation x=x0sin2ωt. The motion simple harmonic
View SolutionFigure shows the circular motion of a particle. The radius of the circle, the period, same of revolution and the initial position are indicated on the figure. The simple harmonic motion of the x-projection of the radius vector the rotating particle P is
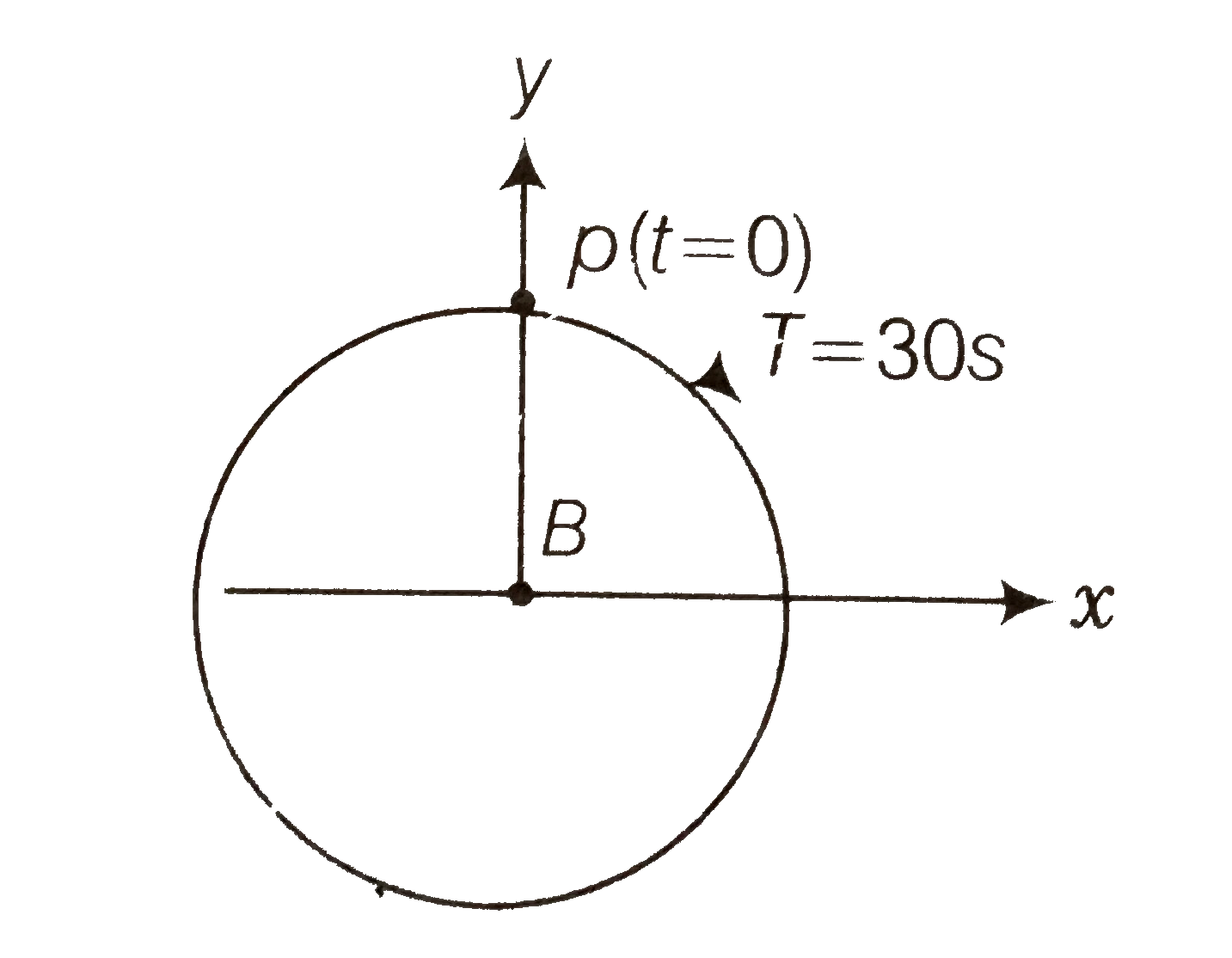
View Solutionthe circular motion of a particle. The radius of the circle, the period, sense of revolution and the initial position are indicated on the figure. The simple harmonic motion of the x-projection of the radius vector of the rotating particle P is
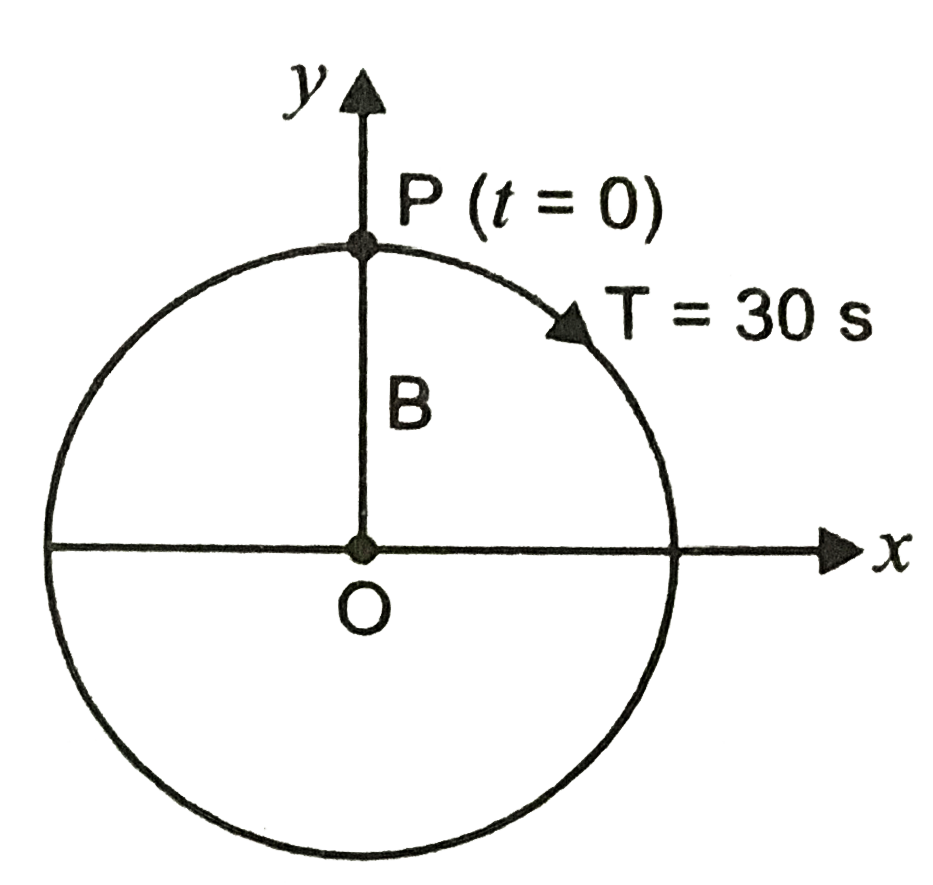
View Solution

