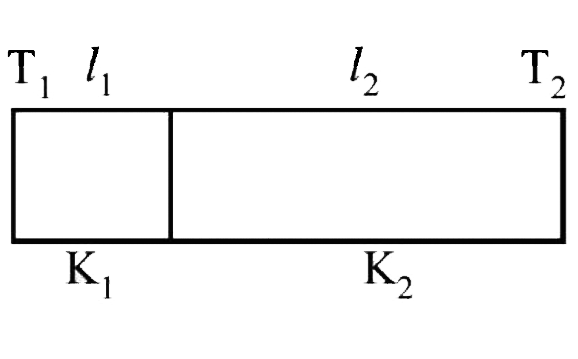
One end of thermally insulated rod is kept at a temperature $T_{1}$ and the other at $T_{2}$ . The rod is composed of two section of length $l_{1}$ and $l_{2}$ thermal conductivities $k_{1}$ and $k_{2}$ respectively. The temerature at the interface of two section is

A

$(K_{2} l_{2} T_{1} + K_{1} l_{1} T_{2}) / (K_{1} l_{1} + K_{2} l_{2})$

B

$(K_{2} l_{1} T_{1} + K_{1} l_{2} T_{2}) / (K_{2} l_{1} + K_{1} l_{2})$

C

$(K_{1} l_{2} T_{1} + K_{2} l_{1} T_{2}) / (K_{1} l_{2} + K_{2} l_{1})$

D

$(K_{1} l_{1} T_{1} + K_{2} l_{2} T_{2}) / (K_{1} l_{1} + K_{2} l_{2})$

Video Solution

Text Solution

Verified by Experts

The correct Answer is:C

Let the temperature of the interface be $T_{0}$ .
Thermal current = $\frac{Temperature difference}{Thermal resitance}$
Thermal resistance = $\frac{1}{K} \frac{l}{A}$
$\Rightarrow \frac{T_{1} - T_{0}}{l_{1} / K_{1} A} = \frac{T_{0} - T_{2}}{l_{2} / K_{2} A}$
$\Rightarrow T_{0} = \frac{K_{1} l_{2} T_{1} - K_{2} l_{1} T_{2}}{K_{1} l_{2} + K_{2} l_{1}}$

|

Updated on:21/07/2023

Class 12 PHYSICS RAY OPTICS AND OPTICAL INSTRUMENTS

Topper's Solved these Questions

Similar Questions

Knowledge Check

Question 1 - Select One
One end of a thermally insulated rod is kept at a temperature $T_{1}$ and the other at $T_{2}$ . The rod is composed of two sections of length $l_{1} and l_{2}$ and thermal conductivities $K_{1} and K_{2}$ respectively. The temperature at the interface of the two section is

A $\frac{K_{1} l_{1} T_{1} + K_{2} l_{2} T_{2}}{K_{1} l_{1} + K_{2} l_{2}}$
B $\frac{K_{2} l_{2} T_{1} + K_{1} l_{1} T_{2}}{K_{1} l_{1} + K_{2} l_{2}}$
C $\frac{K_{2} l_{1} T_{1} + K_{1} l_{2} T_{2}}{K_{2} l_{1} + K_{1} l_{2}}$
D $\frac{K_{1} l_{2} T_{1} + K_{2} l_{1} T_{2}}{K_{1} l_{2} + K_{2} l_{1}}$
Question 2 - Select One
Two rods of the same length and diameter, having thermal conductivities $K_{1}$ and $K_{2}$ , are joined in parallel. The equivalent thermal conductivity to the combinationk is
A $\frac{K_{1} K_{2}}{K_{1} + K_{2}}$
B $K_{1} K_{2}$
C $\frac{K_{1} + K_{2}}{2}$
D $\sqrt{K_{1} K_{2}}$
Question 3 - Select One
Two rods $A$ and $B$ are of equal lengths. Their ends of kept between the same temperature and their area of cross-section are $A_{1}$ and $A_{2}$ and thermal conductivities $K_{1}$ and $K_{2}$ . The rate of heat transmission in the two rods will be equal, if
A $K_{1} A_{2} = K_{2} A_{1}$
B $K_{1} A_{1} = K_{2} A_{2}$
C $K_{1} = K_{2}$
D $K_{1} A_{1} = K_{2} A_{2}$

ALLEN-GEOMETRICAL OPTICS-EXERCISE - 05 (A)

Home
Ask Doubt
Profile