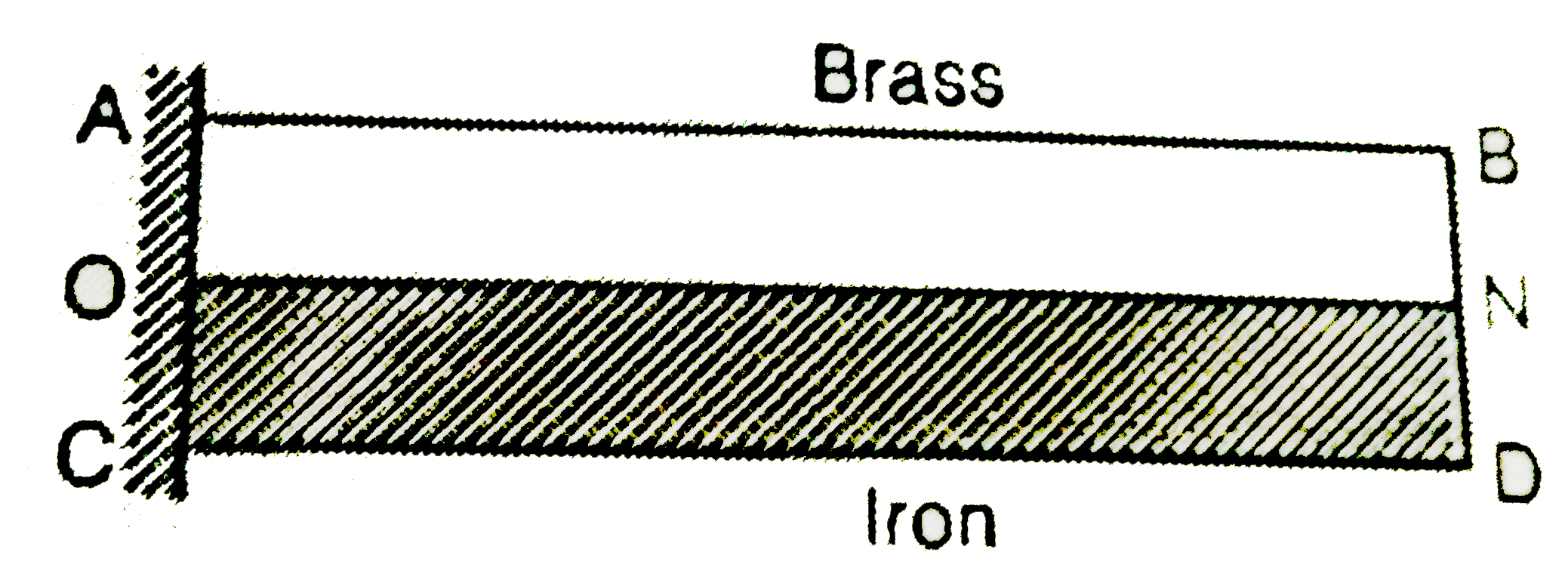
A bimetallic strip of thickness d and length $L$ is clamped at one end at temperature $t_{1}$ . Find the radius of curvature of the strip if it consists of two different metals of expansivity $α_{1}$ and $α_{2} (α_{1} > α_{2}$ ) when its temperature rises to $t_{2}^{\circ} C$ .

Video Solution

Text Solution

Verified by Experts

The correct Answer is: $\frac{d}{(α_{1} - α_{2}) (t_{2} - t_{1})}$

Updated on:21/07/2023

When a strip made or iron $(α_{1})$ and copper $(α_{2}), (α_{2} > α_{1})$ is heated
Aits length does not change
Bit gets twisted
Cit bends with iron on concave side
Dit bends with iro on convex side
A bimetallic strip is composed of two identical strips, one of steel and other of brass. When the temperature of the strip is raised by $Δ T$ , it bends to form arc of curvature R. If the coefficients of linear expansion of steel and brass are $α_{1}$ and $α_{2}$ , respectively, then R is
Adirectly proportional to $| α_{1} - α_{2} |$
Binversely proportional to $| α_{1} - α_{2} |$
Cdirectly proportional to $Δ T$
DNONE OF THESE
A bimetallic strip is formed out of two identical strips one of copper and the other of brass. The co-efficients of linear expansion of the two metals are $α_{C}$ and $α_{B}$ . On heating, the the strip bends to form an are of radius of curvature $R$ . Then $R$ is
Aproportional to $Δ T$
Binversely proportional to $Δ T$
Cproportional to $| α_{B} - α_{C} |$
DInversely proportional to $| α_{B} - α_{C} |$