Statement-1: Temperature of a rod is increased and again cooled to same initial temperature then itsfinal length is equal to original length provided there is no deformation take place.
Statement-2: For a small temperature change , length of a rod varies as l=l0(1+αΔT) provided αΔT<<1. Here symbol have their usual meaning.
Statement -1 is True , Statement -2 is True , Statement -2 is correct explanation for Statement - 1
Statement -1 is True , Statement -2 is True , Statement -2 is not correct explanation for Statement - 1
Statement -1 is True , Statement -2 is False.
Statement -1 is False , Statement -2 is True.
The correct Answer is:B
Step by step video, text & image solution for Statement-1: Temperature of a rod is increased and again cooled to same initial temperature then itsfinal length is equal to original length provided there is no deformation take place. Statement-2: For a small temperature change , length of a rod varies as l = l_(0)(1+alphaDeltaT) provided alpha DeltaT ltlt1. Here symbol have their usual meaning. by Physics experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Topper's Solved these Questions
- GEOMETRICAL OPTICSBook:ALLENChapter:GEOMETRICAL OPTICSExercise:Comprehension Based Questions
Explore 66 Videos
- GEOMETRICAL OPTICSBook:ALLENChapter:GEOMETRICAL OPTICSExercise:EXERCISE - 04 (A)
Explore 48 Videos
- GEOMETRICAL OPTICSBook:ALLENChapter:GEOMETRICAL OPTICSExercise:EXERCISE -03
Explore 11 Videos
- CURRENT ELECTRICITYBook:ALLENChapter:CURRENT ELECTRICITYExercise:All Questions
Explore 427 Videos
- GRAVITATIONBook:ALLENChapter:GRAVITATIONExercise:EXERCISE 4
Explore 9 Videos
Similar Questions
If the temperature of a rod is increased by 10∘C, its length increases by 1 %. What is the percentage change in volume of the body of the same material for 10∘C increase in temperature ?
View SolutionA cylindrical rod of length l, thermal conductivity k and area of cross section A has one end in a furnace maintained at constant temperature. The other end of the rod is exposed to surrounding. The curved surface of the rod is well insulated from the surrounding. The surrounding temperature is T0 and the furnace is maintained at T1=T0+ΔT1. The exposed end of the rod is found to be slightly warmer then the surrounding with its temperature maintained T2=T0+ΔT2[ΔT2<<T0]. The exposed surface of the rod has emissivity e. Prove that ΔT1 is proportional to ΔT2 and find the proportionality constant.
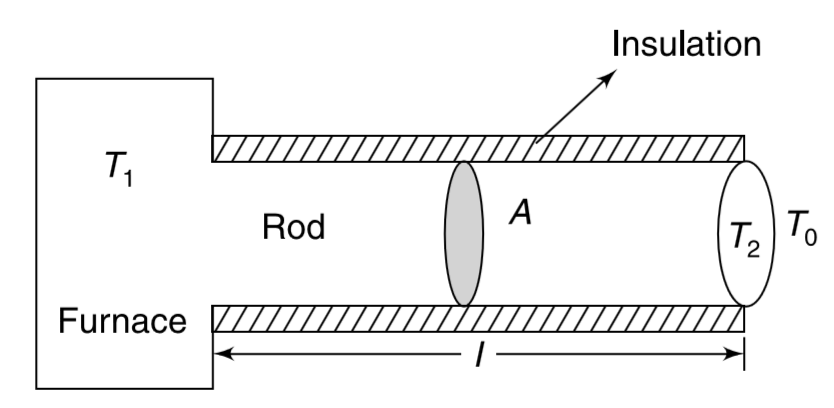
View Solution
Knowledge Check
A thin wire of length l when heated to a certain temperature increases its length by 1%. A sheet of the same material of area 2l×l is heated to the same temperature then percentage increase in area will be :-
A4%B2.5%C2%D1.5%The coefficient of linear expansion of a rod is α and its length is L. The increase in temperature required to increase its legnth by 1% is
A1αB110αC150αD1100αA rod of length l and coefficient of linear expansion α. Find increase in length when temperature changes from T to T+ ΔT
AlαΔTBl(1+αΔT)Cl(1+2αΔT)Dnone of these
A rod of length l and coefficient of linear expansion α. Find increase in length when temperature changes from T to T+ ΔT
View SolutionA copper rod of 88 cm and an aluminium rod of unknown length have their increase in length independent of increase in temperature. The length of aluminium rod is (αcu=1.7×10−5K−1 and αAl=2.2×10−5K−1)
View SolutionA copper rod of 88 cm and an aluminium rod of unknown length have their increase in length independent of increase in temperature. The length of aluminium rod is (αcu=1.7×10−5K−1 and αAl=2.2×10−5K−1)
View SolutionSTATEMENT-1: The temperature of a metallic rod is raised by a temperature At so that its length becomes double. The value of a (coefficient of linear expansion) is given ln2Δt because
STATEMENT-2: Coefficient of linear expansion is defined as 1ldldt
View SolutionStatement I: The expanded length l of a rod of original length l0 is not correctly given by (assuming α to be constant with T) l=l0(1+αΔT) if αΔT is large.
Statement II: It is given by l=l0eαΔT, which cannot be treated as being approximately equal to l=l0(1+αΔT) for large value a ΔT.
View Solution

