n moles of an ideal triatomic linear gas undergoes a process in which the temperature changes with volume as T=K1V2 where K1 is a constant. Choose incorrect alternative.
At normal temperature Cv=52R
At any temperature Cp−Cv=R
At normal temperature molar heat capacity C=3R
At any temperature molar heat capacity C=3R
The correct Answer is:D
At normal temperature Cv=f2R=52R
At any temperature Cp−Cv=(f2+1)−f2R=R from process T=k1V2 and
Ideal gas equation PV=nRT
we have PV−1 = constant ⇒x=−1
⇒C=Cv+R1−x=Cv+R1+1=Cv+R2
At normal temperature
C=52R+R2=3R
Topper's Solved these Questions
- GEOMETRICAL OPTICSBook:ALLENChapter:GEOMETRICAL OPTICSExercise:EXERCISE -03
Explore 11 Videos
- GEOMETRICAL OPTICSBook:ALLENChapter:GEOMETRICAL OPTICSExercise:ASSERTION-REASON
Explore 40 Videos
- GEOMETRICAL OPTICSBook:ALLENChapter:GEOMETRICAL OPTICSExercise:EXERCISE -01
Explore 65 Videos
- CURRENT ELECTRICITYBook:ALLENChapter:CURRENT ELECTRICITYExercise:All Questions
Explore 427 Videos
- GRAVITATIONBook:ALLENChapter:GRAVITATIONExercise:EXERCISE 4
Explore 9 Videos
Similar Questions
One mole of an ideal gas goes through a process in which the entropy of the gas changes with temperature T as S=aT+CV1nT, where a is a positive constant. CV is the molar heat capacity of this gas at constant volume. Find the volume dependence of the gas temperature in this process if T=T0 at V=V0.
View SolutionOne mole of an ideal monoatomic gas at 1 atm, 300 K undergo a process in which pressure of gas is 8 atm then calculate W (in cal).
View Solution
Knowledge Check
n moles of an ideal gas undergo a process in which the temperature changes with volume as T=kv2. The work done by the gas as the temperature changes from 70 to 470 is
A3nRT0B(52)nRT0C(32)nRT0DZeroA gas undergoes a process in which its pressure P and volume V are related as VPn= constant. The bulk modulus of the gas in the process is:
AnPBP1/nCP/nDPnOne mole of an ideal monoatomic gas under goes a process V=aT2. The temperature of the gas increases by 100K. Which of the following is incorrect ?
Athe work done by the gas in the process is 200R JouleBthe molar heat capacity for the process is 7R2Cfor the process PT2= constantDfor the process coefficient of volume expansion is γ=2T
One mole of a monoatomic ideal gas undergoes a thermodynamic process such thatV3T2= constant. Then,
View SolutionFor a monoatomic ideal gas undergoing an adiabatic change, the relation between temperature and volume is TVx = constant, where x is
View SolutionFor a monoatomic ideal gas undergoing an adiabatic change, the relation between temperature and volume TVx = constant, where x is
View Solutionn' moles of an ideal gas undergoes a process A→B as shown in the figure. The maximum temperature of the gas during the process will be:
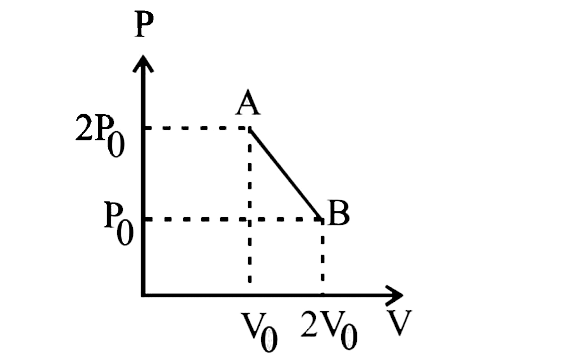
View SolutionOne mole of an ideal monotomic gas undergoes a linear process from A to B in which its pressure p and its volume V change as shown in figure.
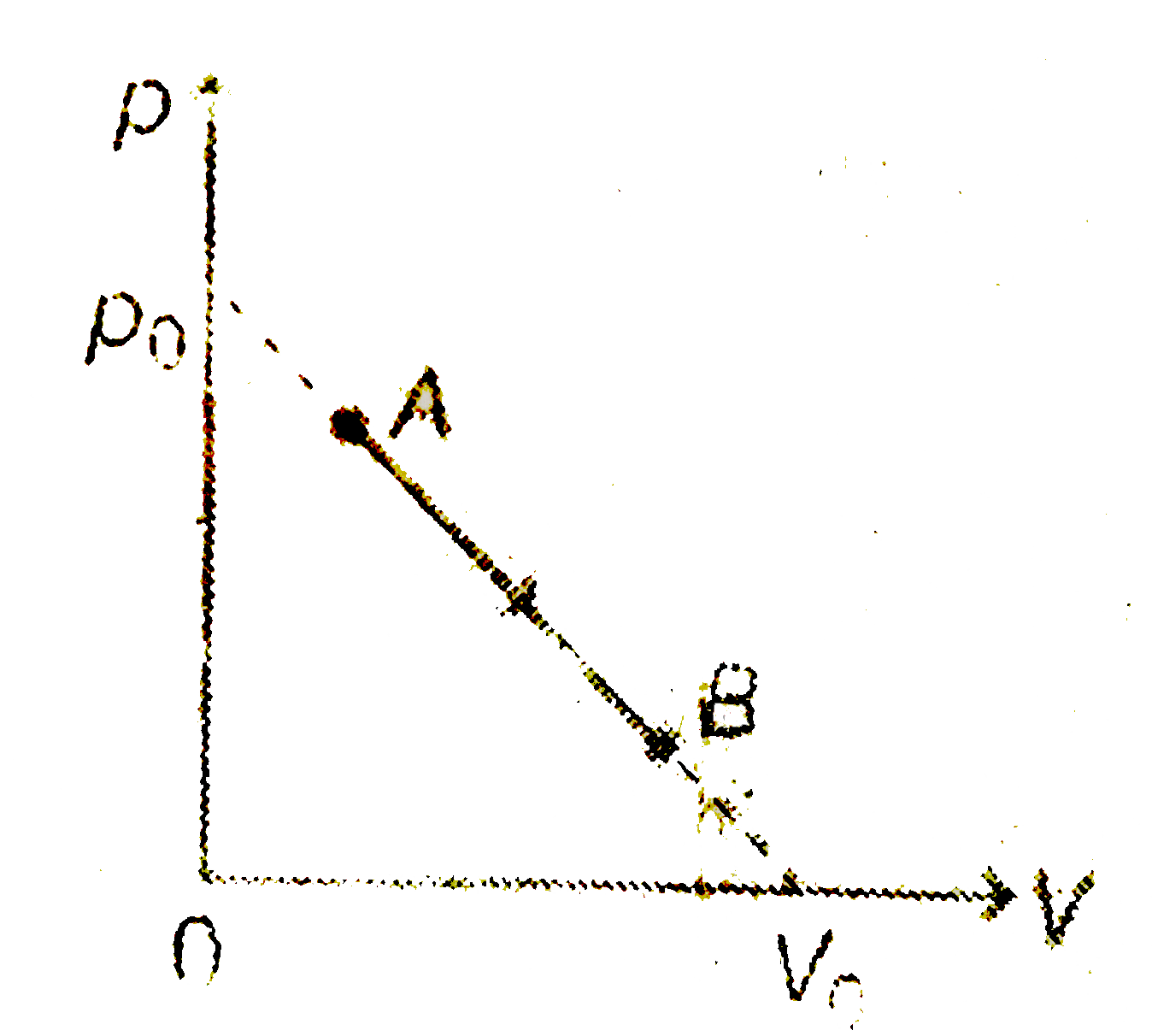
The absolute temperature T versus volume V for the given process is
View Solution

