1023 molecules of a gas strike a target of area 1m2 at angle 45∘C to normal and rebond elastically with speed 1kms1. The impulses normal to wall per molecule is " - [Given : mass of molecule = 3.32×10−27kg]
4.7×10−24kgms−1
7.4×10−24kgms−1
3.32×10−24kgms−1
2.33kgms−1
The correct Answer is:A
Change in momentum
= 2mvcos(45∘)
= 2×3.32×10−24×103×1√2
= 4.7×10−24kgms−1,
_E01_053_S01.png)
Topper's Solved these Questions
- GEOMETRICAL OPTICSBOOK - ALLENCHAPTER - GEOMETRICAL OPTICSEXERCISE - EXERCISE -02
82 Videos
- GEOMETRICAL OPTICSBOOK - ALLENCHAPTER - GEOMETRICAL OPTICSEXERCISE - EXERCISE -03
11 Videos
- GEOMETRICAL OPTICSBOOK - ALLENCHAPTER - GEOMETRICAL OPTICSEXERCISE - SOME WORKED OUT EXAMPLES
84 Videos
- CURRENT ELECTRICITYBOOK - ALLENCHAPTER - CURRENT ELECTRICITYEXERCISE - All Questions
427 Videos
- GRAVITATIONBOOK - ALLENCHAPTER - GRAVITATIONEXERCISE - EXERCISE 4
9 Videos
Similar Questions
The mass of hydrogen molecule is 3.23×1023 hydrogen molecules strike 2cm2 of a wall per second at an angle of 45∘ with the normal when moving with a speed of 105cms−1, what pressure do they exert on the wall ? Assume collision to be elasitc.
View SolutionA molecules in a gas container hits the wall with speed 200m/s at an angle 30∘ with the normal, and reboudns with the same speed. Is momentum conserved in the collision ? Is the collision elastic or inelastic ?
View Solution
Knowledge Check
A ball of mass 0.1 kg strikes a wall normally with a speed of 30ms−1 and rebounds with a speed of 20ms−1. The impulse of the force exerted by the wall on the ball is
A1N−sB5N−sC2N−sD3N−sThe mass of hydrogen molecule is 3.32×10−27 kg. If 1023 hydrogen molecules strick per second at 2 cm2 area of a rigid wall at an angle of 45∘ from the normal and rebound back with a speed of 1000 ms−1, then the pressure ezxeted on the wass is
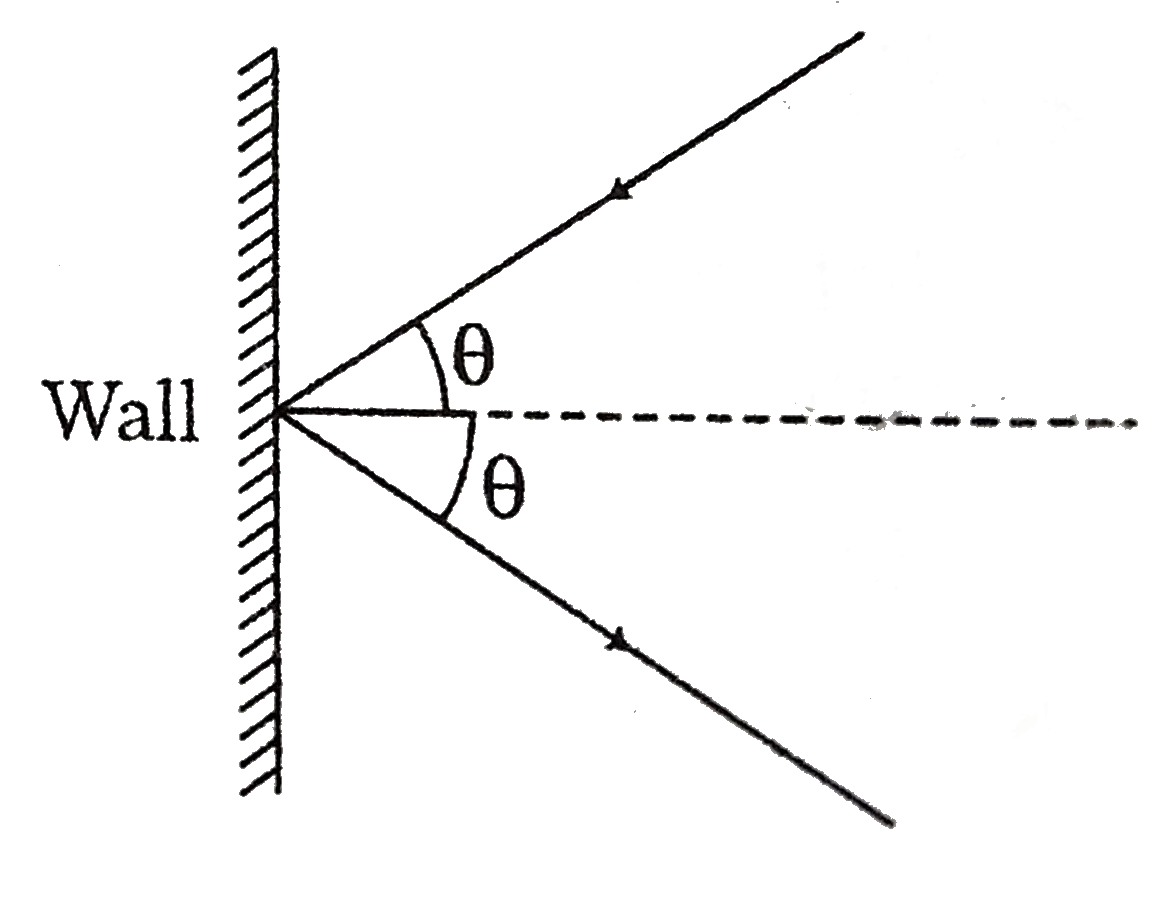A2.34×103 PaB0.23×106PaC0.23×103PaD23.4×103PaGas molecules each of mass 10−26 kg are taken in a container of volume 1dm3 . The root mean square speed of gas molecules is 1 km sec−1 .What is the temperature fo gas molecules.
(Given : NA=6×1023,R=8J/mol.K)A298 KB25 KC250 KD2500 K
Calculate the KE per molecule and also rms velocity of a gas at 127∘C. Given k=1.38×10−23Jmolecule−1K−1 and mass of each molecule =6.4×10−27kg.
View SolutionA nitrogen molecules at teh surface of earth happens to have the rms speed for that gas at 0∘. If it were to go straight up without colliding with other molecules, how high would it rise? Mass of nitrogen molecules, m=4.65×1026lg,k=1.38×10−23Jmolecule−1K−1.
View SolutionFour molecules of a gas have speed 1,2,3and4kms−1 respectively. The value of rms speed of the molecules is (in kms−1)
View Solution1023 molecules of a gas, each having a mass of 3×10−27 kg strike per second per sq. cm. of a rigid will at an angle of 60∘ with the normal and rebound with a velocity of 500m/s. What is the pressure exerted by the gas molecules on the wall?
View Solution1022 gas molecules each of mass 10−26 M collide with a surface (perpendicular to it) elastically per second over an area 1m2 with a speed 104ms−1, the pressure exerted by the gas molecules will be of the order of:
View Solution