Derive the expression for moment of inerita of a uniform disc about an axis passing through the centre and perpendicular to the plane.Solution in Tamil
Let us consider a disc of mass M and radius R. It is found that this disc is made up of many infinitesimally small rings as shown in the figure. Consider one such ring of mass (dm) and thickness (dr) and radius (r). The moment of inerita (dI) of this small ring is given by
dI=(dm)r2
As the mass is uniformly distributed the mass per unit area (σ) is σ=massarea=MπR2
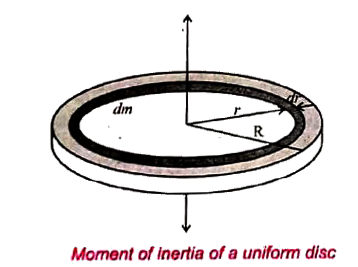
The mass of the infinitesimaly small ring is given by
dm=σ2πrdr−MπR22πrdr
where tehh term (2πrdr) is the area of this elemental ring where 2πr is the length and dr is the thickness.
∴dm=2MR2rdr
∴dI=2MR2r3dr
The moment of inertia (I) of the entire disc is,
I=∫dI
I=∫R02MR2r3dr=2MR2∫R0r3dr
K=2MR2[r44]R0=2MR2[R44−0]
I=12MR2
Topper's Solved these Questions
- MOTION OF SYSTEM OF PARTICLES AND BODIESBook:PREMIERS PUBLISHERSChapter:MOTION OF SYSTEM OF PARTICLES AND BODIESExercise:TEXTBOOK QUESTIONS & ANSWERS (CONCEPTUAL QUESTIONS)
Explore 16 Videos
- MOTION OF SYSTEM OF PARTICLES AND BODIESBook:PREMIERS PUBLISHERSChapter:MOTION OF SYSTEM OF PARTICLES AND BODIESExercise:TEXTBOOK QUESTIONS & ANSWERS (NUMERICAL PROBLEMS)
Explore 12 Videos
- MOTION OF SYSTEM OF PARTICLES AND BODIESBook:PREMIERS PUBLISHERSChapter:MOTION OF SYSTEM OF PARTICLES AND BODIESExercise:TEXTBOOK QUESTIONS & ANSWERS (SHORT ANSWER QUESTIONS)
Explore 34 Videos
- LAW OF MOTION Book:PREMIERS PUBLISHERSChapter:LAW OF MOTION Exercise:OTHER IMPORTANT QUESTIONS & ANSWERS (VI Numerical Problems)
Explore 62 Videos
- NATURE OF PHYSICAL WORLD AND MEASUREMENTBook:PREMIERS PUBLISHERSChapter:NATURE OF PHYSICAL WORLD AND MEASUREMENTExercise:OTHER IMPORTANT QUESTIONS & ANSWERS (III. Short Answer Questions.)
Explore 24 Videos
Similar Questions
When a tree is cut, the cut is made on the side facing the direction in which the tree is required to fall. Why?
View SolutionA uniform disc of mass 100 g has a diameter of 10 cm. Calculate the total energy of the disc when rolling along a horizontal table with a velocity of 20 cm s−1. (take the surface of table as reference).
View SolutionDefine the center of mass of a body.
View SolutionA scooterist moving with a speed of 36mkmh−1 sees a child standing in the middle of the raod he applies the brakes and brings the scooter to rest in 5s just in time to saved child calculate the average retarding force on the vehicle if mass of the vehicle and drive is 300 kg
View SolutionWhat is meant by Parallax?
View SolutionDerive an expression for moment of inertia of a thin circular ring about an axis passing through its centre and perpendicular to the plane of the ring.
View SolutionState the expression for the moment of inertia of a thin uniform disc about an axis perpendicular to its plane and through its centre. Hence deduce the expression for its moment of inertia about a tangential axis perpendicular to its plane.
View SolutionThe moment of inertia of a copper disc, rotating about an axis passing through its centre and perpendicular to its plane
View SolutionDerive the expression for moment of inertia of a uniform ring about an axis passing thorugh the centre and perpendicular to the plane.
View SolutionDerive the expression for moment of inerita of a uniform disc about an axis passing through the centre and perpendicular to the plane.
View SolutionDerive the expression for moment of inerita of a uniform disc about an axis passing through the centre and perpendicular to the plane.
View SolutionDerive the expression for moment of inerita of a uniform disc about an axis passing through the centre and perpendicular to the plane.
View SolutionFind the moment of inertia of a uniform half-disc about an axis perpendicular to the plane and passing through its centre of mass. Mass of this disc is M and radius is R.
View SolutionDerive the expression for moment of inertia of a uniform ring about an axis passing thorugh the centre and perpendicular to the plane.
View SolutionDerive the expression for moment of inertia of a uniform ring about an axis passing thorugh the centre and perpendicular to the plane.
View Solution

