A small body tied to one end of the string is whirled in a vertical circle. Find the velocity and tension at the lowest and highest point of the circle respectively. Solution in Tamil
Let a body of mass (m) attached to one end of a massless and inextensible string. It executes circular motion in a vertical plane with the other end of the string which is fixed. The length of the string becomes the radius of the circular path as shown in the figure (motion in vertical circle).
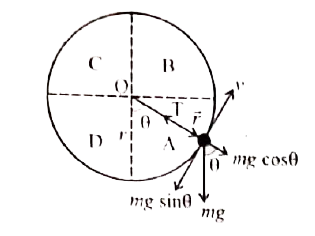
Let us discuss the motion of the body by taking the free body diagram (FBD) at a position where the position vector makes an angle with the vertically downward direction. The instantaneous velocity is as shown in figure. There are two forces acting on the mass. They are
(i) Gravitational force that acts downward.
(ii) Tension acts along the string.
Applying Newton's second law on the mass, in the tangential direction, we get
where, is tangential retardation In the radial direction,
Where, is the centripetal acceleration
Let the circle can be divided into four sections A, B, C, D for better understanding of the motion. The four important facts to be understood from the two equations are as follows:
(i) The mass is having tangential acceleration for all values of (except ), from this it is clear that this vertical circular motion is not a uniform circular motion.
(iii) From the equations (1) and (2) it is understood that as the magnitude of velocity is not a constant in the course of motion, the tension in the string is also not constant.
(iii) The equation (2), highlights that in sections A and D of the circle, (for is positive), the term is always greater than zero. Hence the tension cannot be vanished even when the velocity vanishes.
(iv) The equation (2), , further highlights that in sections B and C of the circle, (for is negative) the second term is always greater than zero. Hence velocity cannot be vanished, even when the tension is vanished.
The important points which are to be kept in mind are related to motion in vertical circle.
(a) To start with let us consider only two positions, say the lowest point 1 and the highest point 2 as shown in the figure for further analysis.
(b) Let the velocity of the body at the lowest point 1 be , at the highest point 2 be and at any other point.
(c ) The direction of velocity is tangential to the circular path at all points.
(d) Let be the tension in the string at the lowest point let be the tension at the highest point and be the tension at any other point.
(e) Tension at each point acts towards the centre. The tensions and velocities at these two points can be found by applying the law of conservation of energy.
For the lowest point (1): When the body is at the lowest point 1, the gravitational force that acts on the body vertically downwards and another one is the tension acting vertically upwards, i.e., towards the centre. From the equation (2), we get
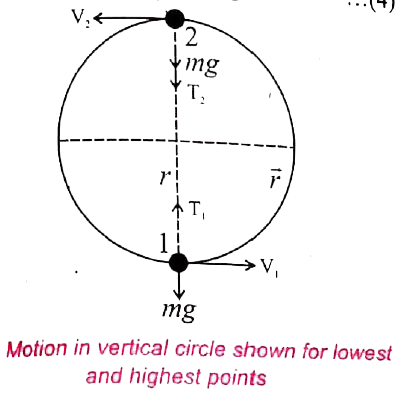
For the highest point (2): At the highest point 2, both the gravitational force on the body and the tension act downwards, i.e., towards the centre again.
From equations (4) and (5), it is understood that .
By subtracting equation (6) from equation (4). The difference in tension is obtained.
The term can be found easily by applying law of conservation of energy at point 1 and also at point 2.
But total energy at point is same as the total energy at a point
Potential energy at point 1, (by taking reference as point 1)
Kinetic energy at point 1,
Total energy at point 1,
Similarly, potential energy at point 2,
( from point 1)
Kinetic energy at point 2,
Total energy at pont 2,
From the law of conservation of energy given in equation (8), we get
After rearranging,
Substituting equatoin (9) in equation (7) we get,
Hence, the difference in tension is
Minimum speed at the highest point (2): The body must have a minimum speed at point 2 otherwise, the string will slack before reaching point 2. So the body will not loop the circle. To find this minimum speed let us take the tension in equation (6).
The body must have a speed at point 2, to stay in the circular path.
Minimum speed at the lowest pont 1: To have this minimum speed at point 2, the body must have minimum speed also at point 1.
By making use of equation (9) we can find the minimum speed at point 1.
Substituting equation (10) in (8),
Related Playlists
- BOOK - PREMIERS PUBLISHERSCHAPTER - WORK, ENERGY AND POWER EXERCISE - NUMERICAL PROBLEMS76videos
WORK, ENERGY AND POWER
- BOOK - PREMIERS PUBLISHERSCHAPTER - WORK, ENERGY AND POWER EXERCISE - CONCEPTUAL QUESTIONS34videos
WORK, ENERGY AND POWER
- BOOK - PREMIERS PUBLISHERSCHAPTER - WORK, ENERGY AND POWER EXERCISE - SHORT ANSWER QUESTIONS42videos
WORK, ENERGY AND POWER
- BOOK - PREMIERS PUBLISHERSCHAPTER - WAVESEXERCISE - OTHER IMPORTANT & QUESTIONS ANSWERS ( NUMERICAL PROBLEMS. )48videos
WAVES
Similar Questions
Calculate the work done by a force of 30 N in lifting load of 2g to a height of 10 m (g=10ms−2).
03:43View SolutionA spring which is initially in un-streatched condition, is first stretched by a length x and again by a further length x. The work done in the first case W1 is one third of the work done in second case W2. True of false ?
02:17View SolutionExplain how the definition of work in physics is different from general perception.
04:05View SolutionThe equation of a wave is,
y(x,t)=0.05sin[π2(10x−40t)−π4]m Find,
The wavelength, the frequency and the wave velocity.
(ii) The particle velocity and acceleration at x=0.5 m and t=0.05 s.09:13View SolutionA stone is tied to one end of a string and rotated in a vertical circle . What is the difference in tensions of the string at lowest and highest points of the vertical circle ?
View SolutionIF a stone is tied to one end of the string and whirled in verticle circle, then the tension in the string at the lowest point is equal to
04:09View SolutionIf a bodyy is tied to a string and whirled in vertical circle, then the tension in the string at the highest position is
07:56View Solutionएक पत्थर रस्सी के एक सिरे से बाँधकर ऊर्ध्वाधर वृत्त में घुमाया जाता है | ऊर्ध्वाधर वृत्त के निम्नतम और उच्चतम बिंदुओं पर रस्सी के तनावों का अंतर कितना होगा ?
09:59View SolutionA body tied to one end of a string is made to revolve in a vertical circle. Derive an expression for the velocity of the body and tension in the string at any point.
View SolutionA stone of mass 1kg is tied with a string and it is whirled in a vertical circle of radius 1 m. If tension at the highest point is 14 N, then velocity at lowest point will be
04:12View Solution0.3 किग्रा. द्रव्यमान की एक गेंद 0.8 मीटर लम्बी डोरी के एक सिरे से बाँधकर ऊर्ध्वाधर वृत्त में घुमायी जाती है। वृत्त के उच्चतम बिन्दु पर गेंद की न्यूनतम चाल ज्ञात कीजिए। वृत्त के निम्नतम बिन्दु पर डोरी में कितना तनाव होगा?
View Solution0.5 किग्रा. का एक पिण्ड 50 सेमी. लम्बी डोरी के एक सिरे पर बाँधकर ऊर्ध्व वृत्त में घुमाया जाता है। यदि वृत्त के निम्नतम बिन्दु पर पिण्ड की चाल 6 मी./से. हो तो वृत्त के उच्चतम बिन्दु पर पिण्ड की न्यूनतम चाल ज्ञात कीजिए। उच्चतम व निम्नतम बिन्दुओं पर डोरी में तनाव क्या होगा?
View SolutionThe maximum and minimum tensions in a string of length 0.1m with a stone 5g tied to it and whirled in a vertical circle are in the ratio 13:1. The velocity of the body at highest point is:
View SolutionA stone of mas 1 kg is tied to one end of a string of length 0.5 m. It is whirled in a vertical circle. If the maximum tension in the string is 58.8 N, the velocity at the top is
View SolutionThe maximum and minimum tensions in a string of length 0.1m with a stone 5g tied to it and whirled in a vertical circle are in the ratio 13:1. The velocity of the body at highest point is
04:03View Solution


