Use the graph to find the limits (if it exists).If the limit does not exist ,explain why?
limx→1f(x)
where f(x)={x2+2x≠11x=1
Text Solution
The correct Answer is:3
|
Topper's Solved these Questions
- DIFFERENTIAL CALCULUS LIMITS AND CONTINUITYBook:PREMIERS PUBLISHERSChapter:DIFFERENTIAL CALCULUS LIMITS AND CONTINUITYExercise:SOLUTION TO EXERCISE 9.2
Explore 15 Videos
- DIFFERENTIAL CALCULUS LIMITS AND CONTINUITYBook:PREMIERS PUBLISHERSChapter:DIFFERENTIAL CALCULUS LIMITS AND CONTINUITYExercise:SOLUTION TO EXERCISE 9.3
Explore 13 Videos
- DIFFERENTIAL CALCULUS LIMITS AND CONTINUITYBook:PREMIERS PUBLISHERSChapter:DIFFERENTIAL CALCULUS LIMITS AND CONTINUITYExercise:PROBLEMS FOR PRACTICE
Explore 58 Videos
- DIFFEREMTIAL CALCULUS DIFFERENTIABILITY AND METHODS OF DIFFERENTITAION Book:PREMIERS PUBLISHERSChapter:DIFFEREMTIAL CALCULUS DIFFERENTIABILITY AND METHODS OF DIFFERENTITAION Exercise:PROBLEMS FOR PRACTICE
Explore 73 Videos
- EXAMINATION QUESTION PAPER MARCH 2019Book:PREMIERS PUBLISHERSChapter:EXAMINATION QUESTION PAPER MARCH 2019Exercise:PART -IV
Explore 4 Videos
Similar Questions
Knowledge Check
Evaluate the following limits:
limx→12(4x2−12x−1)A−1B1C2D0
Evaluate the following limits, if they exist :
limx→3[x(x+1)]
View SolutionEvaluate the limits, if exist(lim)x→0log(1+x3)sin3x
View SolutionFind the limits :
limx→1{x2+x+1x3+1}
View SolutionEvaluate the following limits, if they exist :
limx→1(x3−x2+1)
View SolutionConsider the following graph of the function y=f(x). Which of the following is//are correct?
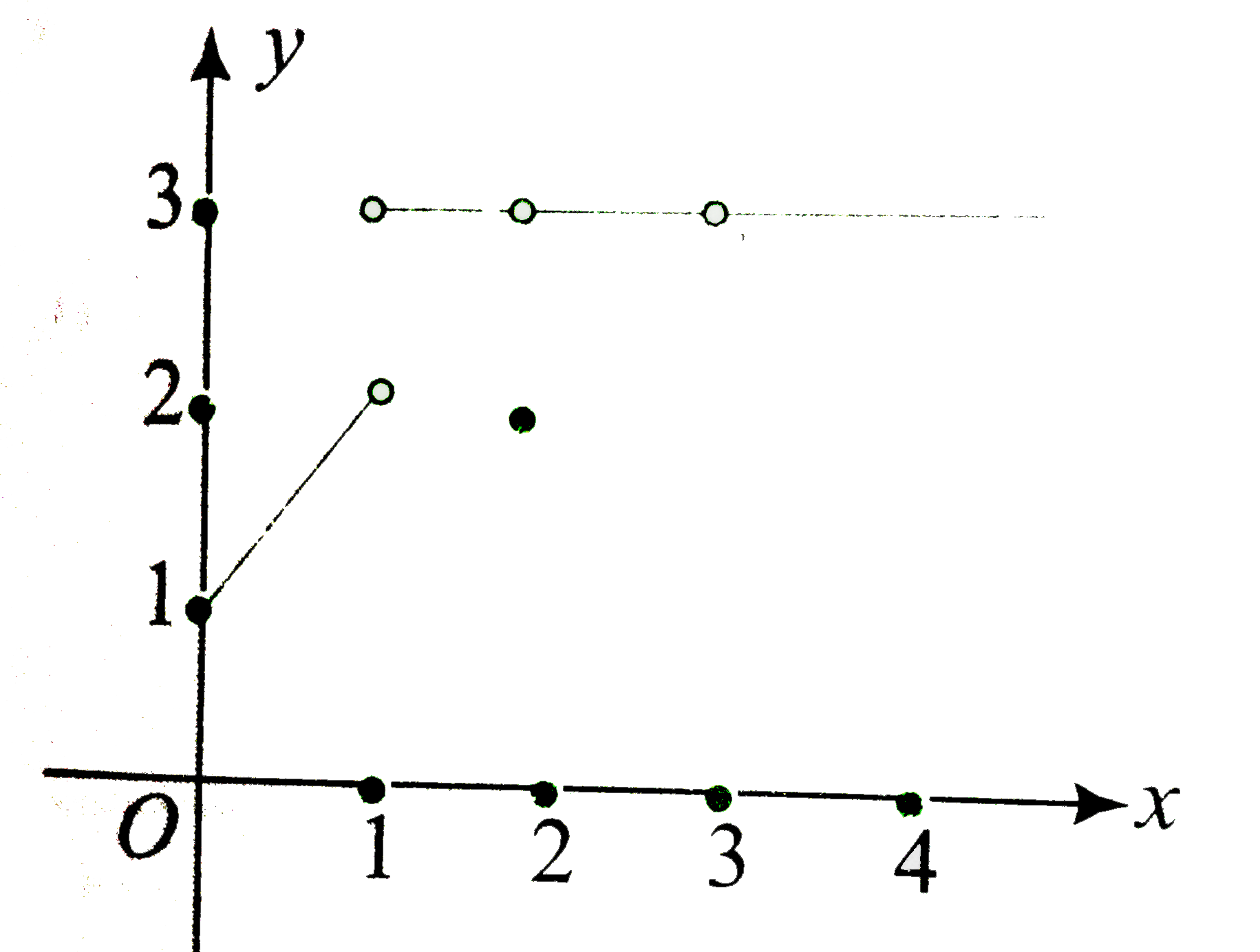
(a)limx→1f(x) does not exist.
(b)limx→2f(x) does not exist.
(c)limx→3f(x)=3.
(d)limx→1.99f(x)exists.
View SolutionConsider the following graph of the function y=f(x). Which of the following is//are correct?

(a)limx→1f(x) does not exist.
(b)limx→2f(x) does not exist.
(c)limx→3f(x)=3.
(d)limx→1.99f(x)exists.
View SolutionFind the following limits :
limx→1⎧⎨⎩x15−1x1100−1⎫⎬⎭
View Solution

