यह दर्शाइए कि किसी ठोस की आयताकार शीट का क्षेत्र प्रसार गुणांक $\frac{Δ A / A}{Δ T}$ , इसके रैखिक प्रसार गुणांक $α$ का दो गुना होता है।

Video Solution

Text Solution

Verified by Experts

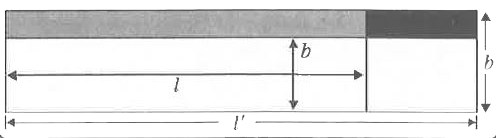
माना आयताकार शीट की लम्बाई l एवं चौड़ाई b है तब $Δ T$ ताप वृद्धि करने के पश्चात नयी लम्बाई
$l ’ = l + Δ l$ होगी
$l ’ = ’ + l α Δ T = l (1 + α Δ T)$
इसी तरह से चौड़ाई $b ’ = b + Δ b$ होगी
$b ’ = b + b α Δ T$
$b ’ = b (1 + α Δ T)$
जहां $α$ शीट के पदार्थ का रेखीय प्रसार गुणांक है। अतः ताप वृद्धि के पश्चात क्षेत्रफल
$A ’ = l ’ b ’ = l (1 + α Δ T) b (1 + α Δ T)$
$A ’ = l b {(1 + α Δ T)}^{2}$
$A ’ = A (1 + 2 α Δ T + α^{2} {(Δ T)}^{2})$
यहां $A = l b =$ शीट का प्रारंभिक क्षेत्रफल है। चूंकि $α$ का मान 1 से बहुत कम होता है और $Δ T$ अलप है अतः इनके वर्ग के पद $α^{2} {(Δ T)}^{2}$ को नगण्य माना जा सकता है।
अतः $A ’ = A (1 + 2 α D \leq t a T) = A + 2 A α T$
$\Rightarrow$ क्षेत्रफल में वृद्धि $Δ A = A^{1} - A$
$= A + 2 A α D e < A T - a$
$= 2 A α Δ T$
क्षेत्रफल प्रसार गुणांक $β = \frac{Δ A}{A Δ T}$
$= \frac{2 A α Δ T}{A Δ T} = 2 α$

|

Updated on:21/07/2023

Class 11 PHYSICS FLUID MECHANICS

Topper's Solved these Questions

Similar Questions

SANJEEV PUBLICATION-द्रव्य के तापीय गुण-गत वर्षों की विभिन्न प्रतियोगी परीक्षाओं में पूछे गये प्रश्न

Home
Ask Doubt
Profile