Question

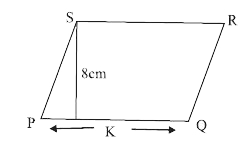
The area of a parallelogram PQRS is $36c{m}^2$. M is any point on the side RS. The area of $\Delta PMQ$ is.

Options

A. `18 cm^(2)`
B. `9 cm^(2)`
C. `36 cm^(2)`
D. `12 cm^(2)`

Answer

A

Explanation

To find the area of triangle PMQ given that the area of parallelogram PQRS is 36 cm², we can follow these steps:

1. Understand the Given Information:
- The area of parallelogram PQRS is given as 36 cm².
- M is any point on the side RS of the parallelogram.

2. Identify the Relationship:
- The area of a parallelogram can be calculated using the formula:
\( \text{Area} = \text{Base} \times \text{Height} \)
- For parallelogram PQRS, we can take PQ as the base and PM as the height.

3. Set Up the Equation:
- Let the length of base PQ be \( b \) and the height PM be \( h \).
- From the area of the parallelogram, we have:
\( b \times h = 36 \text{ cm}^2 \)

4. Calculate the Area of Triangle PMQ:
- The area of triangle PMQ can be calculated using the formula:
\( \text{Area of } \Delta PMQ = \frac{1}{2} \times \text{Base} \times \text{Height} \)
- Here, the base is PQ (which is \( b \)) and the height is PM (which is \( h \)).
- Substituting the values, we get:
\( \text{Area of } \Delta PMQ = \frac{1}{2} \times b \times h \)

5. Substitute the Area of the Parallelogram:
- Since we know that \( b \times h = 36 \text{ cm}^2 \), we can substitute this into the triangle area formula:
\( \text{Area of } \Delta PMQ = \frac{1}{2} \times 36 \text{ cm}^2 = 18 \text{ cm}^2 \)

6. Final Answer:
- Therefore, the area of triangle PMQ is:
\( \text{Area of } \Delta PMQ = 18 \text{ cm}^2 \)