The difference of any two sides of a triangle is _______ than the third side .
The correct Answer is:less
To solve the question, we need to understand a fundamental property of triangles regarding their sides.
1. Understanding the Triangle Inequality Theorem:
The triangle inequality theorem states that for any triangle, the sum of the lengths of any two sides must be greater than the length of the third side. This can be expressed as:
- a+b>c
- a+c>b
- b+c>a
2. Considering the Difference of Two Sides:
Let's denote the sides of the triangle as a, b, and c. We can consider the difference between any two sides, say a and b. The difference can be expressed as |a−b|.
3. Applying the Triangle Inequality:
According to the triangle inequality theorem, we know that:
- a+b>c
- Rearranging this gives us a+b−c>0 or a+b>c.
- Similarly, we can derive that |a−b|<c. This means that the absolute difference between any two sides of the triangle is less than the length of the third side.
4. Conclusion:
Therefore, we can conclude that the difference of any two sides of a triangle is always less than the third side.
Final Answer:
The difference of any two sides of a triangle is less than the third side.
The triangle inequality theorem states that for any triangle, the sum of the lengths of any two sides must be greater than the length of the third side. This can be expressed as:
- a+b>c
- a+c>b
- b+c>a
Let's denote the sides of the triangle as a, b, and c. We can consider the difference between any two sides, say a and b. The difference can be expressed as |a−b|.
According to the triangle inequality theorem, we know that:
- a+b>c
- Rearranging this gives us a+b−c>0 or a+b>c.
- Similarly, we can derive that |a−b|<c. This means that the absolute difference between any two sides of the triangle is less than the length of the third side.
Therefore, we can conclude that the difference of any two sides of a triangle is always less than the third side.
The difference of any two sides of a triangle is less than the third side.
Topper's Solved these Questions
- TRIANGLESBOOK - CBSE COMPLEMENTARY MATERIALCHAPTER - TRIANGLESEXERCISE - PART-A (State which of the following statements are true and false )
5 Videos
- TRIANGLESBOOK - CBSE COMPLEMENTARY MATERIALCHAPTER - TRIANGLESEXERCISE - PART-B
10 Videos
- TRIANGLESBOOK - CBSE COMPLEMENTARY MATERIALCHAPTER - TRIANGLESEXERCISE - PRACTICE TEST
8 Videos
- SURFACE AREAS AND VOLUMESBOOK - CBSE COMPLEMENTARY MATERIALCHAPTER - SURFACE AREAS AND VOLUMESEXERCISE - Practice Test
8 Videos
Similar Questions
The sum of any two sides of a triangle is _______ than the third side .
View SolutionShow that the difference of any two sides of a triangle is less than the third side. Given : A ABC To Prove: (i) AC−AB<BC BC−AC<AB (iii) BC−AB<AC Construction: Take point D on AC such that AD=AB . Join BD
View Solution
Knowledge Check
Assertion : If a line divides any two sides of a triangle in the same ratio , then the line is paralle to third side .
Reason : Line segment joining the mid -point of any two sides of a triangle is parallel to the third side .AIf both assertion and reason are true and reason is the correct explanation of assertion .BIf both assertion and reason are true but reason is not the correct explanation of assertion .CIf assertion is true reason is false .DIf assertion is false but reason is true .
Show that the difference of any two sides of a triangle is less than the third side. GIVEN : ABC TO PROVE : (i) AC−AB<BC BC−AC<AB (iii) BC−AB<AC CONSTRUCTION : Take a point D on AC such that AD=AB. Join BD.
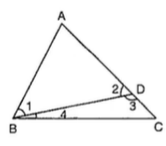
View SolutionShow that the difference of any two sides in a triangle is smaller than the third side.
View SolutionFill in the blanks to make the following statements true: In a right triangle the hypotenuse is the ...... side. The sum of three altitudes of a triangle is ......... than its perimeter. The sum of any two sides of a triangle is ......... than the third side. If two angles of a triangle are unequal, then the smaller angle has the ........... side opposite to it. Difference of any two sides of a triangle is ......... than the third side. If two sides of a triangle are unequal, then the larger side has ..... angle opposite to it.
View SolutionSum of any two sides of a triangle is greater than the third side.
View SolutionSum of any two sides of a triangle is not less than the third side
View SolutionThe sum of any two sides of a triangle is greater than third side.
View SolutionThe sum of any two sides of a triangle is always ...... than the third side.
View Solution
