A spiral is made up of successive semicircles, with centres alternately at A and B, starting with centre at A, of radii 0.5 cm, 1.0 cm, 1.5 cm, 2.0 cm, . . . as shown in Figure. What is the total length of such a spiral made up of thirteen consecutive
semicircles? (Take π=227)

Video Solution
Text Solution
Circumference of the semicircle = 12×2πr=πr
Circumference of first semicircle = π×0.5
Circumference of second semicircle = π×1.0
Circumference of third semicircle = π×1.5
And so on Circumference of 13th semicircle = π×6.5
Hence, series with common difference of 0.5π
Hence, sum of the series is
S=n2(a+l)
S=132(0.5π+6.5π)
S=45.5π
Thus, length of spiral is = 45.5π
=227×45.5
=143
Length of spiral is 143cm.
|
Similar Questions
Knowledge Check
In a circle with centre at O (0,0) 2. and radius 5 cm, AB is a chord of length 8 cm. If OM is perpendicular to AB, then the length of OM is:
A2.5cm.B3cm.C4cm.D1cm.Two objects A and B are of lengths 5 cm and 7 cm determined with errors 0.1 cm and 0.2 cm respectively. What is the error in determining the total length?
A(12±0.3)cmB12 cmC(2±0.3)cmD(2±0.6)cmThis figure is made up of a semicircle and quarter of a circle. The length of AB=9.1cm. The distance from A to the centre of the semicircle is 3.5 cm. The area of the figure is
 A25cm2B28.26cm2C22.715cm2D88cm2
A25cm2B28.26cm2C22.715cm2D88cm2
What is the angle subtended at the centre of a circle of radius 10 cm by an arc of length 5π cm?
View SolutionAn arc of a circle subtends an angle π at the centre. If the length of the arc is 22 cm, then what is the radius of the circle ? (Take π=227)
View SolutionWhat is the angle subtended at the centre of a circle of radius 5cm by an arc length 4π cm?
View SolutionThree particles of masses 0.5 kg, 1.0 kg and 1.5 kg are placed at the three corners of a right angled triangle of sides 3.0 cm, 4.0 cm and 5.0 cm as shown in figure. Locate the centre of mass of the system.
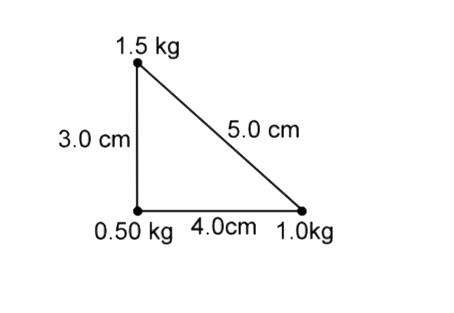
View SolutionThree points masses 1.0 kg , 1.5 kg and 2.5 kg are placed at the vertices of a right-angle triangle of sides 4.0 cm, 3.0 cm and 5.0 cm, as shown in the figure. The centre of mass of the system is
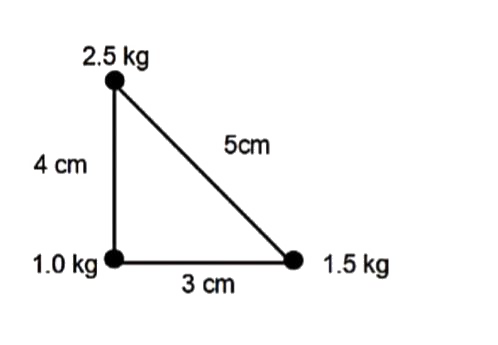
View Solution
