An equiconvex lens of refractive index 1.6 has power 4D in air. Its power in water is:
1.5 D
2.0 D
1.3 D
3.2 D
The correct Answer is:3
To solve the problem, we will use the lensmaker's formula and the concept of power of a lens in different media.
1. Understanding the Given Information:
- The refractive index of the lens (μ_l) = 1.6
- The power of the lens in air (P_air) = 4 D (diopters)
- The refractive index of air (μ_air) = 1.0
- The refractive index of water (μ_water) = 1.33
2. Using the Lensmaker's Formula:
The power of a lens is given by the formula:
P=(μl−μm)⋅1f
where:
- P is the power of the lens,
- μl is the refractive index of the lens,
- μm is the refractive index of the medium,
- f is the focal length of the lens.
3. Finding the Focal Length in Air:
From the power in air:
Pair=(μl−μair)⋅1f
Substituting the values:
4=(1.6−1)⋅1f
4=0.6⋅1f
Rearranging gives:
f=0.64=0.15 m=15 cm
4. Finding Power in Water:
Now we need to find the power of the lens when it is placed in water:
Pwater=(μl−μwater)⋅1f
Substituting the values:
Pwater=(1.6−1.33)⋅10.15
Pwater=0.27⋅10.15
Pwater=0.27⋅6.67≈1.8 D
5. Final Calculation:
Thus, the power of the lens in water is approximately:
Pwater≈1.8 D
Conclusion:
The power of the lens in water is approximately 1.8 D.
---
- The refractive index of the lens (μ_l) = 1.6
- The power of the lens in air (P_air) = 4 D (diopters)
- The refractive index of air (μ_air) = 1.0
- The refractive index of water (μ_water) = 1.33
The power of a lens is given by the formula:
P=(μl−μm)⋅1f
where:
- P is the power of the lens,
- μl is the refractive index of the lens,
- μm is the refractive index of the medium,
- f is the focal length of the lens.
From the power in air:
Pair=(μl−μair)⋅1f
Substituting the values:
4=(1.6−1)⋅1f
4=0.6⋅1f
Rearranging gives:
f=0.64=0.15 m=15 cm
Now we need to find the power of the lens when it is placed in water:
Pwater=(μl−μwater)⋅1f
Substituting the values:
Pwater=(1.6−1.33)⋅10.15
Pwater=0.27⋅10.15
Pwater=0.27⋅6.67≈1.8 D
Thus, the power of the lens in water is approximately:
Pwater≈1.8 D
The power of the lens in water is approximately 1.8 D.
Similar Questions
An equiconvex lens of refractive index μ2 is placed such that the refractive :
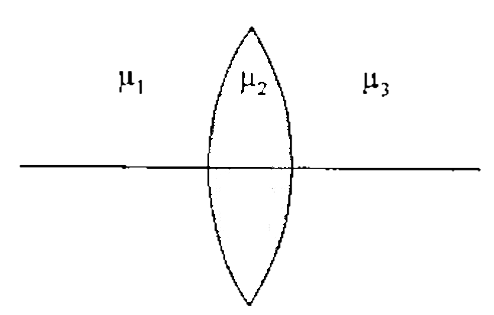
View SolutionA convex lens has a refractive index 1.5 and power 7 diopter. When the lens is immersed in a liquid, it behaves as a concave lens of focal length 120 cm. Calculate the refractive index of the liquid.
View Solution
Knowledge Check
A convex lens of refractive index 3/2 has a power of 2.5∘. If it is placed in a liqud of refractive index 2,the new power of the lens is
A2.5DB−2.5DC1.25DD−1.25DA convex lens (refractive index μ = 1.5) has a power P. If it is immersed in a liquid (μ = 4/3), then its power will become/remain
APBP2CP4D4PA thin convex lens of refractive index 1.5cm has 20cm focal length in air. If the lens in completely immersed in a liquid of refractive index. 1.6, then its focal length will be
A−160cmB−100cmC+10cmD+100cm
A convex lens of refractive index 1.5 has a focal length of 20 cm in air. Calculate the change in its focal length when it is immersed in water of refractive index 4/3.
View SolutionA convex lens of refractive index 1.5 has a focal length of 18 cm in air. Calculate the change in its focal length when it is immersed in water of refraction index 43.
View SolutionA convex lens of refractive index 1.5 has a focal length of 18 cm in air. Calculate the change in its focal length when it is immersed in water of refractive index 43.
View SolutionA thin converging lens of refractive index 1.5 has a focal power of 5 D. When this lens is immersed in a liquid, it acts as a diverging lens of focal length 100 cm. The refractive index of the liquid is
View SolutionAn equiconvex lens of refractive index n2 is placed such that the refractive index of the surrouding media is as shown. The lens :
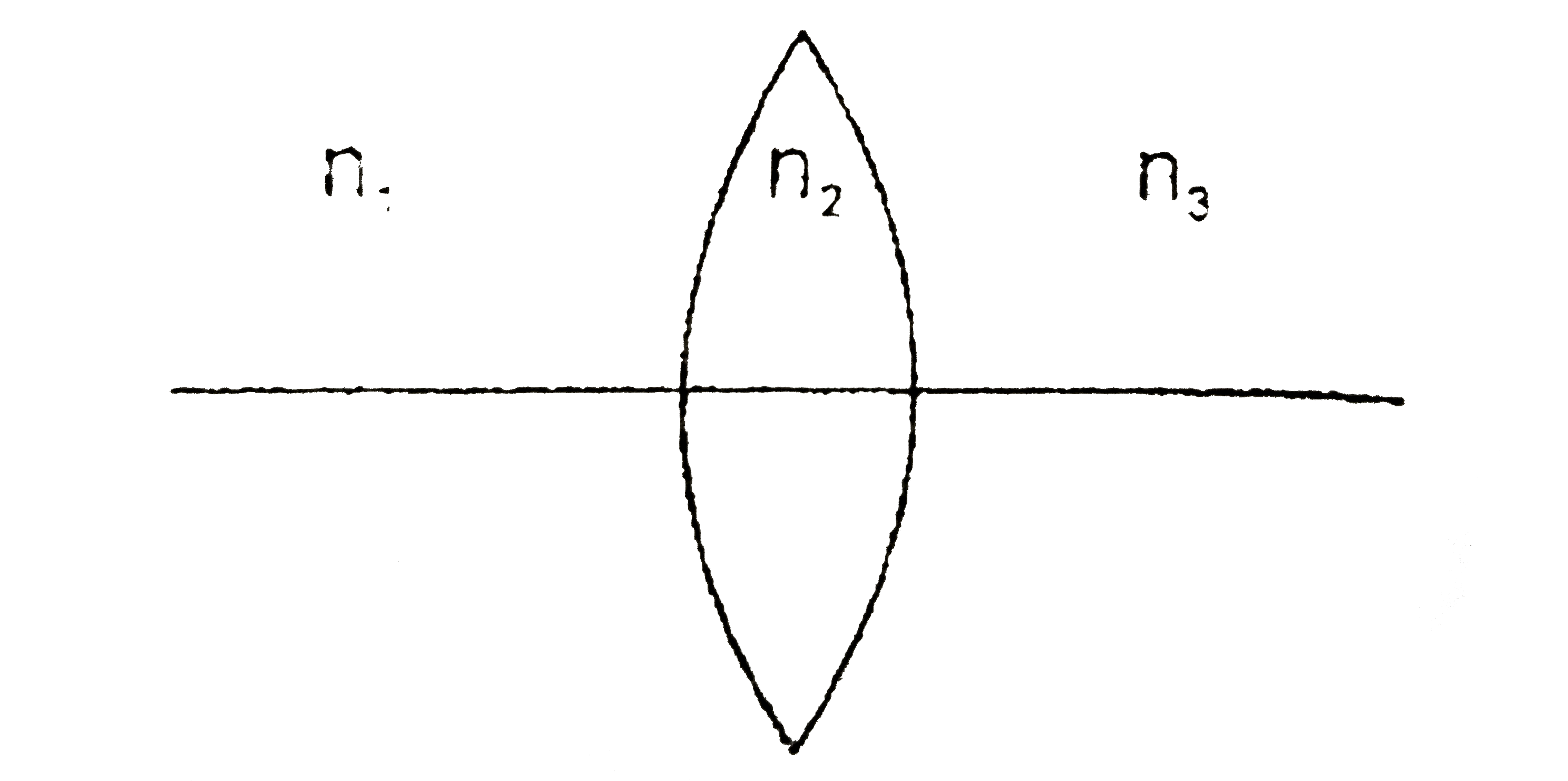
View Solution