Question

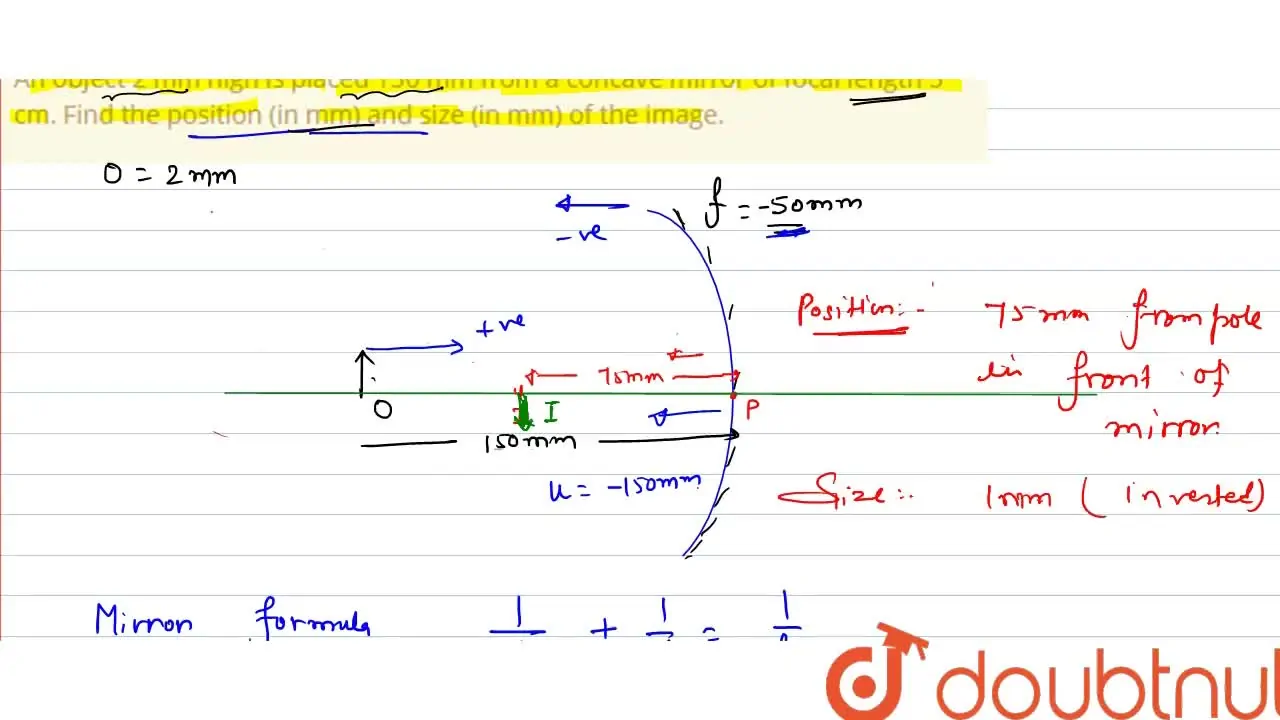
An object 2 mm high is placed 150 mm from a concave mirror of focal length 5 cm. Find the position (in mm) and size (in mm) of the image.

Explanation

To solve the problem of finding the position and size of the image formed by a concave mirror, we will follow these steps:

Step 1: Identify the given values
- Height of the object (h_o) = 2 mm
- Object distance (u) = -150 mm (negative because the object is in front of the mirror)
- Focal length (f) = -50 mm (negative for concave mirrors)

Step 2: Use the mirror formula
The mirror formula is given by:
\( \frac{1}{f} = \frac{1}{v} + \frac{1}{u} \)
Where:
- \( f \) = focal length
- \( v \) = image distance
- \( u \) = object distance

Step 3: Substitute the known values into the mirror formula
Substituting the values into the formula:
\( \frac{1}{-50} = \frac{1}{v} + \frac{1}{-150} \)

Step 4: Rearranging the equation
Rearranging gives:
\( \frac{1}{v} = \frac{1}{-50} + \frac{1}{150} \)

Step 5: Finding a common denominator
The common denominator for -50 and 150 is 150. Thus:
\( \frac{1}{-50} = \frac{-3}{150} \)
So, we have:
\( \frac{1}{v} = \frac{-3 + 1}{150} = \frac{-2}{150} \)

Step 6: Solve for v
Now, solving for \( v \):
\( v = \frac{150}{-2} = -75 \text{ mm} \)

Step 7: Calculate the magnification
The magnification (m) is given by:
\( m = \frac{h_i}{h_o} = -\frac{v}{u} \)
Where:
- \( h_i \) = height of the image
- \( h_o \) = height of the object

Substituting the values:
\( m = -\frac{-75}{-150} = \frac{75}{150} = \frac{1}{2} \)

Step 8: Calculate the height of the image
Now, using the magnification to find the height of the image:
\( h_i = m \cdot h_o = \frac{1}{2} \cdot 2 \text{ mm} = 1 \text{ mm} \)

Final Results
- Position of the image (v) = -75 mm (the negative sign indicates that the image is formed in front of the mirror)
- Size of the image (h_i) = 1 mm (the image is inverted)

Summary
- The image is located at 75 mm in front of the mirror and has a height of 1 mm.

---