An alternating current of rms value 10 A is passed through a resistor. The maximum potential difference across the resistor is:
20V
90V
169.68V
None of these
The correct Answer is:C
To find the maximum potential difference across a resistor when an alternating current (AC) is passed through it, we can follow these steps:
Step 1: Understand the relationship between RMS current and maximum current
The root mean square (RMS) value of current (I_RMS) is related to the maximum current (I_0) by the formula:
I0=√2×IRMS
Step 2: Substitute the given RMS value
Given that the RMS value of the current is 10 A, we can substitute this value into the formula:
I0=√2×10A
Step 3: Calculate the maximum current
Calculating this gives:
I0=√2×10≈1.414×10≈14.14A
Step 4: Use Ohm's law to find the maximum potential difference
The maximum potential difference (V_0) across the resistor can be calculated using Ohm's law:
V0=I0×R
where R is the resistance of the resistor.
Step 5: Substitute the resistance value
Given that the resistance R is 12 Ω, we substitute this value into the equation:
V0=14.14A×12Ω
Step 6: Calculate the maximum potential difference
Calculating this gives:
V0=14.14×12≈169.68V
Final Answer
Thus, the maximum potential difference across the resistor is approximately 169.68 V.
---
The root mean square (RMS) value of current (I_RMS) is related to the maximum current (I_0) by the formula:
I0=√2×IRMS
Given that the RMS value of the current is 10 A, we can substitute this value into the formula:
I0=√2×10A
Calculating this gives:
I0=√2×10≈1.414×10≈14.14A
The maximum potential difference (V_0) across the resistor can be calculated using Ohm's law:
V0=I0×R
where R is the resistance of the resistor.
Given that the resistance R is 12 Ω, we substitute this value into the equation:
V0=14.14A×12Ω
Calculating this gives:
V0=14.14×12≈169.68V
Thus, the maximum potential difference across the resistor is approximately 169.68 V.
Similar Questions
Knowledge Check
An alternating current of rms value 10 A is passed through a 12Ω resistor. The maximum potential difference across the resistor is
A20 VB90 VC169.68 VDnone of theseAn alternating current of rms value 10 A is passed through a 12Ω resistor. The maximum potential difference across the resistor is
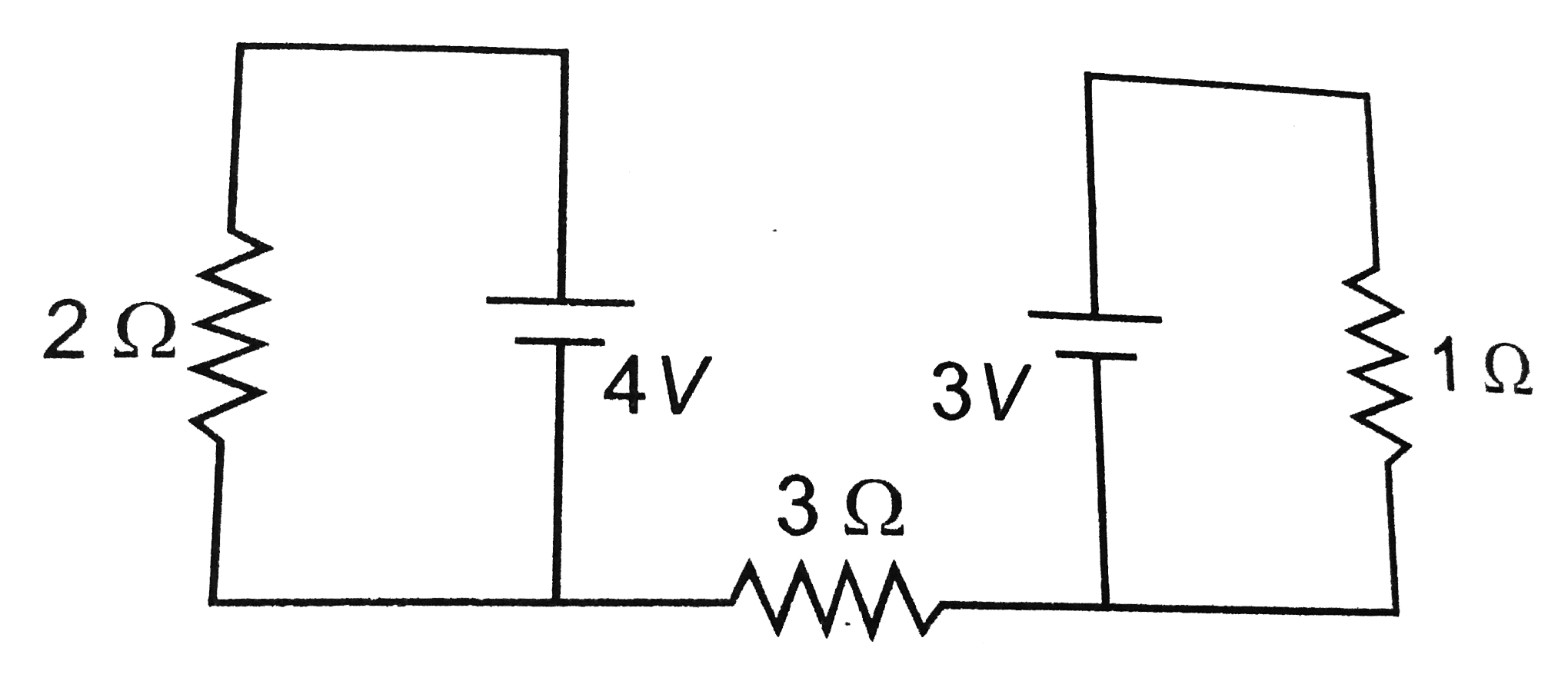
A20 VB90 VC169.68 VDNone of theseThe potential drop across the 3Ω resistor is
 A1VB1.5VC2VD3V
A1VB1.5VC2VD3V
An alternating current of rms value 5A, passes through a resistance of 24Ω. What is the maximum P.D. across the resister?
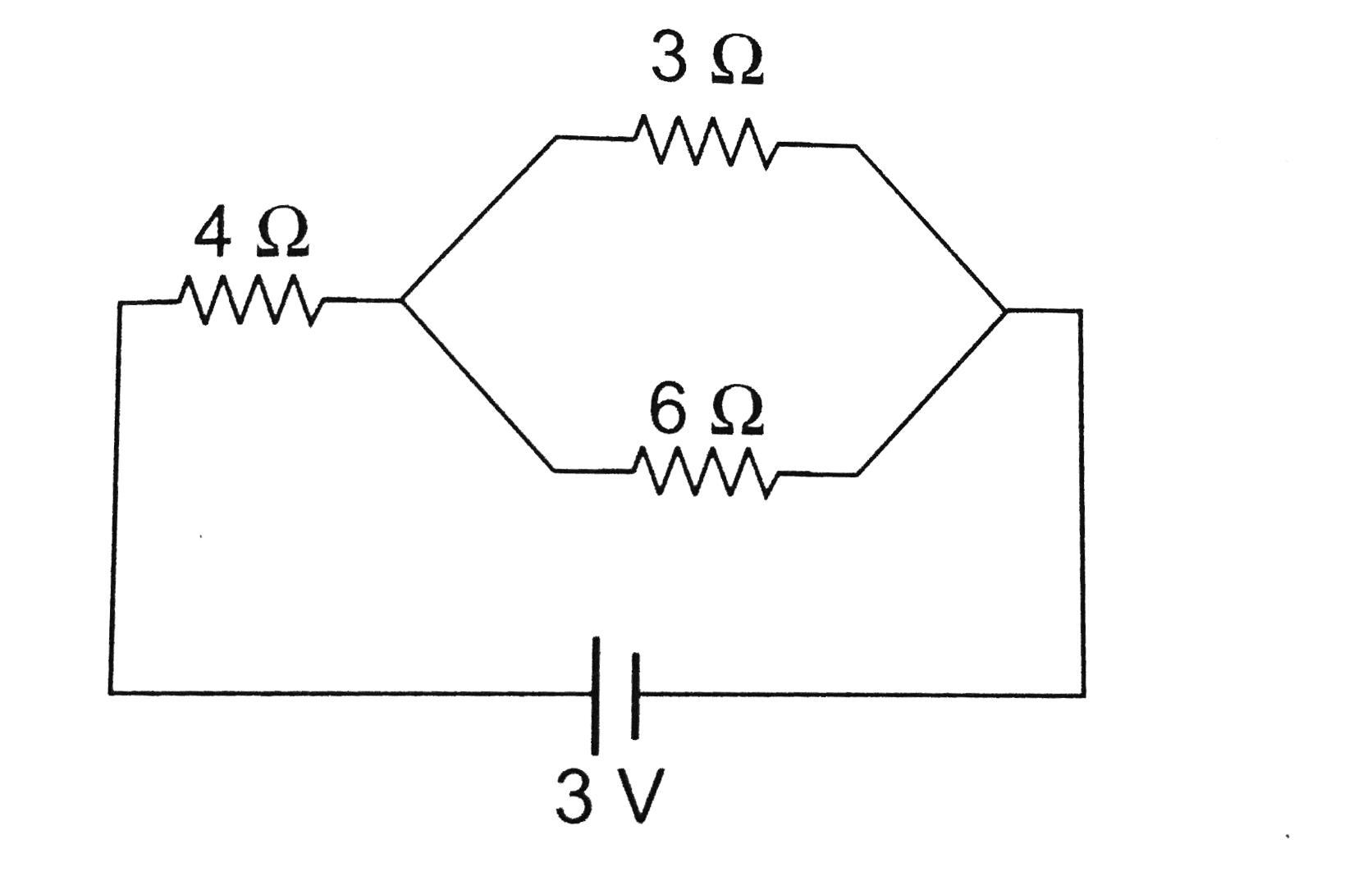
View SolutionIn the circuit shown below:
The potential difference across the 3Ω resistor is:
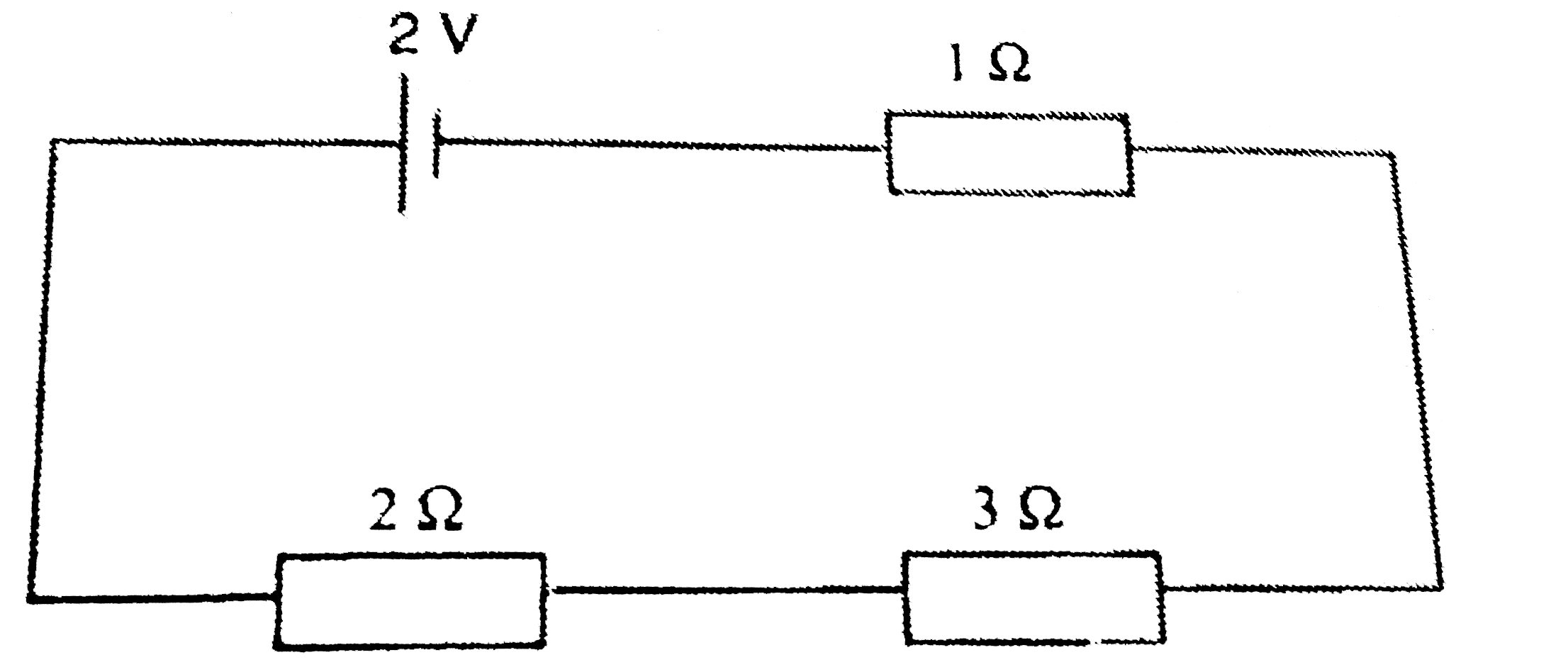
View SolutionCurrent through the 5Ω resistor is
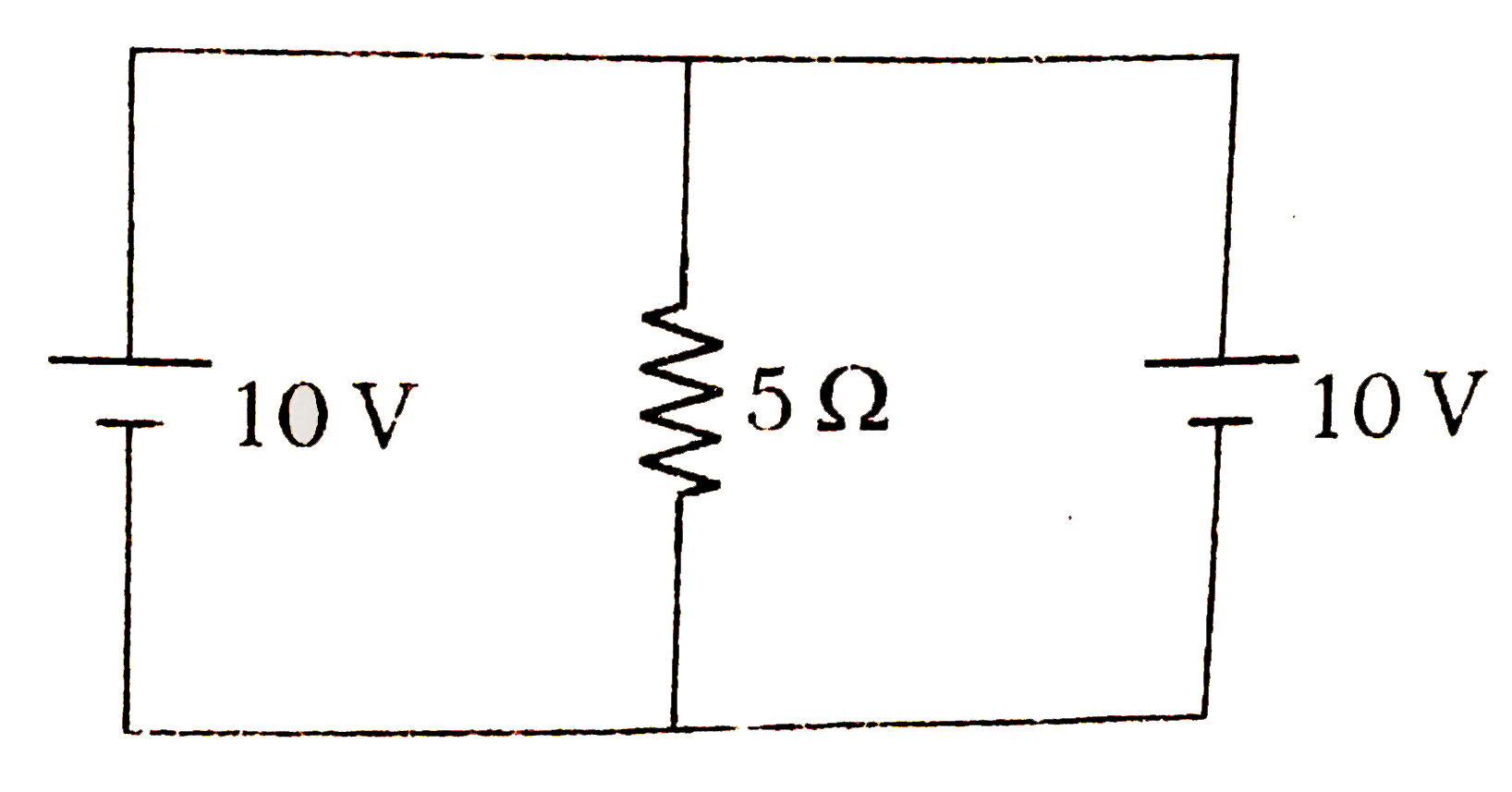
View SolutionCurrent through 3Ω resistor is 0.8A, then potential drop through 4Ω resistor is
View SolutionA 3Ω resistor and a 6Ω resistor are connected in parallel and the combination is connected in series to a battery of 5 V and a 3Ω resistor. The potential difference across the 6Ω resistor
View Solution