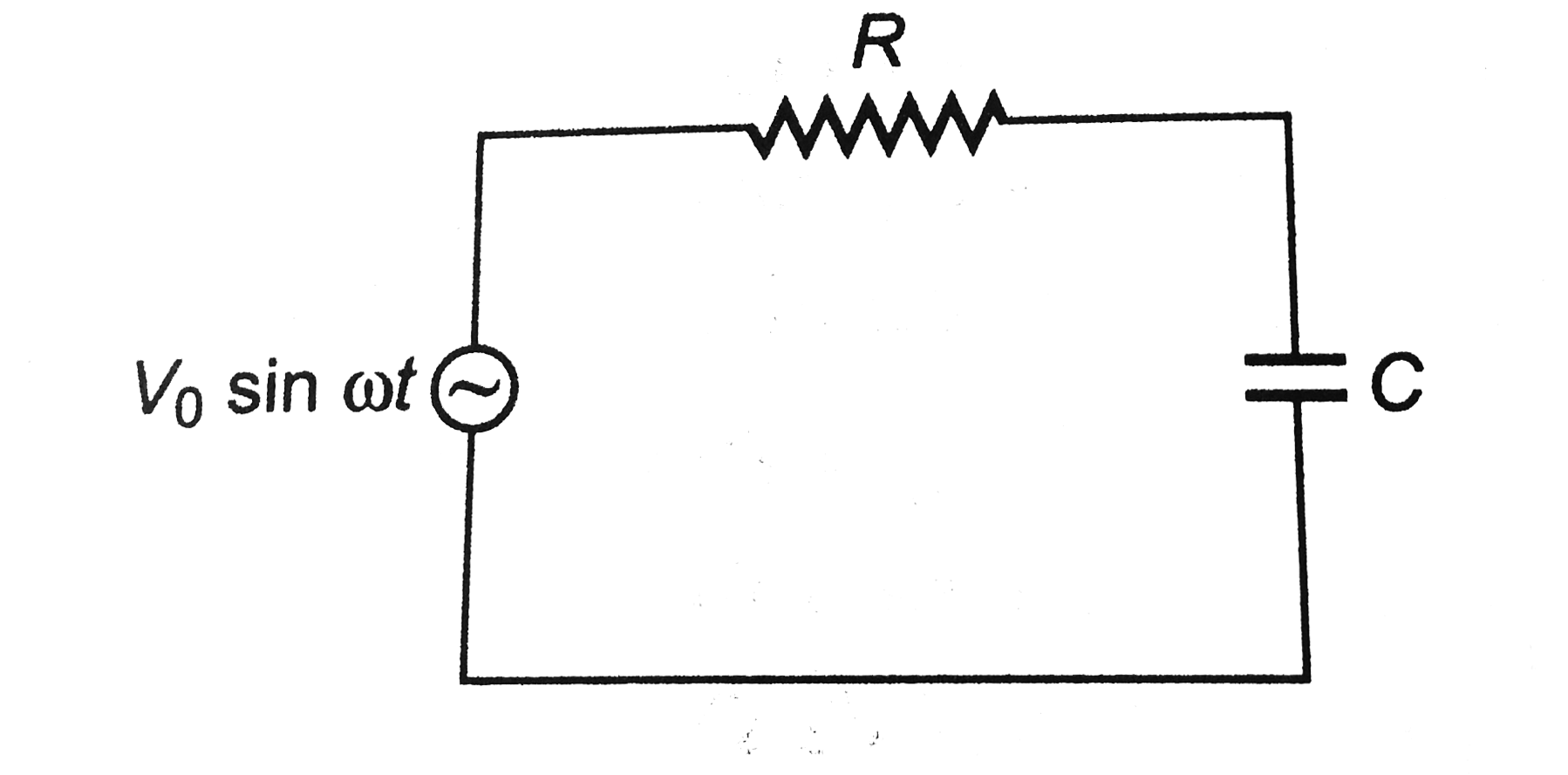
An a.c. source of angular frequency ω is fed across a resistor R and a capacitor C in series. The current registered is I. If now the frequency of the source is changed to ω/3 (but maintaining the same voltage), the current in the circuit is found to be halved. calculate the ratio of reactance to resistance at the original frequency ω.
At angular frequency w, the current in R-C circuit is given by
irms=⎛⎜
⎜
⎜
⎜⎝εrms√(R2)+((1/ω2C2)2(1)
when frequency is changed to w/3, the current is halved.Thus
irms=εrms√(R2)+(1/(ω/3)2C2)=εrms√R2+(9/ω2C2)
From equation (i) and (ii), we have
1√R2+(1/ω2(C2))=2√R2+(9/ω2C2)
Solving this equation, we get3R2=5ω2C2
Hence, the ratio of reactance to resistance is(1/ωC)R=√35
Similar Questions
An ac source of angular frequency ω is fed across a resistor R and a capacitor C in series. The current registered is I. If now the freqency of source is chaged to (ω)/3 (but maintainging the same voltage), the current in the circuit is found to be halved. Calculate the ration of hte reactance to resistance at the original frequency ω.
View SolutionAn a.c. source of angular frequency ω is fed across a resistor R and a capacitor C in series. The current registered is I. If you the frequency of source is changed to ω/3, maintaining the same voltage, current in the circuits is found to be halved. Caculate the ratio of reactance to resistance at the original frequency ω.
View Solution
Knowledge Check
An AC source of angular frequency ω is fed across a resistor R and a capacitor C in series. The current registered is I. If now the frequency of source is changed to ω/3 (but maintaining the same voltage), the current in the circuit is found to be halved. The ratio of reactance to resistance at the original frequency ω will be.
A√35B√53C3/5D5/3An ac source of angular frequency o is fed across a resistor R and a capacitor C in series. The current registered is l. If now the frequency of source is changed to c/3 (but maintaining the same voltage), the current in the circuit is found to be halved. The ratio of reactance to resistance at the original frequency o will be
A√35B√53C3//5D√RAn AC source of frequency ω when fed into a RC series circuit, current is recorded to be l. If now frequency is changed to ω4 (keeping voltage same), the current is found to 1/2. The ratio of reactance to resistance at original frequency ω is
A2B12C1√2DNone of these
An AC source of angular frequency ω is fed across a resistor R and a capacitor C in series. The current registered is l. If now the frequency of source is changed to ω3′ (but maintaining the same voltage), the current in the circuit is found to be halved. The ratio of reactance to resistance at the original frequency is √αβ, Find (α+β)
View SolutionAn AV voltage source is applied across an R-C circuit. Angular frequency of the source is ω, resistance is R and capacitance is C. The current registered is I. If now the frequency of source is changed to ω2 (but maintaining the same voltage), the current in the circuit is found to be two third. calculate the ratio of reactance to resistance at the original frequency ω .
View SolutionResistor of resistance R and capacitor of capacitance C are connected in series to an AC source of angular frequency ω . Rms current in the circuit is I. When frequency of the source is changed to one - third of initial value keeping the voltage same then current is found to be halved. Find the ratio of reactance of capacitor to that with resistance at the original frequency ω .
View SolutionA variable frequency a.c. source is connected to a capacitor. Will the displacement current change if the frequency of the a.c. source is decreased ?
View SolutionAn AC voltage source V=V0siωtis connected across resistance R and capacitance C as shown in figureure. It is given that R=1ωC. The peak current is I0. If the angular frequency of the voltage source is changed to ω√3, then the new peak current in the circuit is
 .
.
View Solution