Two short magnets of equal dipole moments M are fastened perpendicularly at their centres Find the effective magnetic moment.
To find the effective magnetic moment of two short magnets with equal dipole moments M that are fastened perpendicularly at their centers, we can follow these steps:
Step 1: Understanding the Configuration
We have two magnetic dipoles, each with a dipole moment M. They are oriented at a right angle (90 degrees) to each other.
Step 2: Representing the Dipole Moments as Vectors
Since magnetic dipole moments are vector quantities, we can represent them as vectors. Let’s denote the first dipole moment as vector →M1 and the second dipole moment as vector →M2.
- Assume →M1 is along the x-axis.
- Then, →M2 will be along the y-axis.
Step 3: Using Vector Addition
To find the resultant magnetic moment →Mnet, we will add these two vectors. The resultant vector can be found using the vector addition formula for perpendicular vectors:
→Mnet=→M1+→M2
Step 4: Applying the Pythagorean Theorem
Since the two vectors are perpendicular, we can use the Pythagorean theorem to find the magnitude of the resultant vector:
|→Mnet|=√|→M1|2+|→M2|2
Given that both dipole moments are equal, we can substitute |→M1|=M and |→M2|=M:
|→Mnet|=√M2+M2=√2M2
Step 5: Simplifying the Result
This simplifies to:
|→Mnet|=√2M
Conclusion
Thus, the effective magnetic moment of the two short magnets fastened perpendicularly at their centers is:
Effective Magnetic Moment=√2M
We have two magnetic dipoles, each with a dipole moment M. They are oriented at a right angle (90 degrees) to each other.
Since magnetic dipole moments are vector quantities, we can represent them as vectors. Let’s denote the first dipole moment as vector →M1 and the second dipole moment as vector →M2.
- Then, →M2 will be along the y-axis.
To find the resultant magnetic moment →Mnet, we will add these two vectors. The resultant vector can be found using the vector addition formula for perpendicular vectors:
Since the two vectors are perpendicular, we can use the Pythagorean theorem to find the magnitude of the resultant vector:
This simplifies to:
Thus, the effective magnetic moment of the two short magnets fastened perpendicularly at their centers is:
Similar Questions
Knowledge Check
Two short magnets of equal dipole moments M are fastened perpendicularly at their centres as shown in the figure. The magnitude of the magnetic field at a distance d from the centre on the bisector of the right angle is
 Aμ04πMd3Bμ04π√2Md3Cμ04π2√2Md3Dμ04π2Md3
Aμ04πMd3Bμ04π√2Md3Cμ04π2√2Md3Dμ04π2Md3Two short bar magnets of equal dipole moments 'M' each are fastened perpendicular at their centers as shown in figure. The magnitude of the magnetic field at 'P' at a distance d from their common centre as shown in figure is
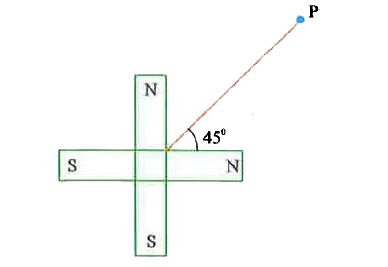 Aμ04πMd3Bμ04π2√2Md3Cμ04π2Md3Dμ02πMd3
Aμ04πMd3Bμ04π2√2Md3Cμ04π2Md3Dμ02πMd3Two short bar magnets are taken and fastened together perpendicularly by their centres as shown in figure. Magnetic moment of each magnet is M and A is a point on bisector of this system at a distance d from the centre as N A S shown in figure. Magnetic field intensity at point A is
 AB=μ04πMd3BB=μ04π2Md3CB=μ04πM√2d3DB=μ04π2√2Md3
AB=μ04πMd3BB=μ04π2Md3CB=μ04πM√2d3DB=μ04π2√2Md3
Magnetic dipole moment is a
View SolutionIf the magnitude of torque is equal to the magnetic dipole moment and the axis of magnet is perpendicular to the field then the magnitude of magnetic induction is
View SolutionTwo short magnets of dipole moment M each are placed crossed at 90∘ (see adjacent figure). The magnetic field at a distance from the centre on the bisector of the right angle is

View SolutionThe magnetic dipole moment has the dimension of
View SolutionTwo identical short magnets having magnetic moment M are placed perpendicular to each other with their , centres coniciding as shown in adjacent figure . The magnitude of the magnetic field at a point P at distance 'd' on the bisector of right angle will be .

View Solution

