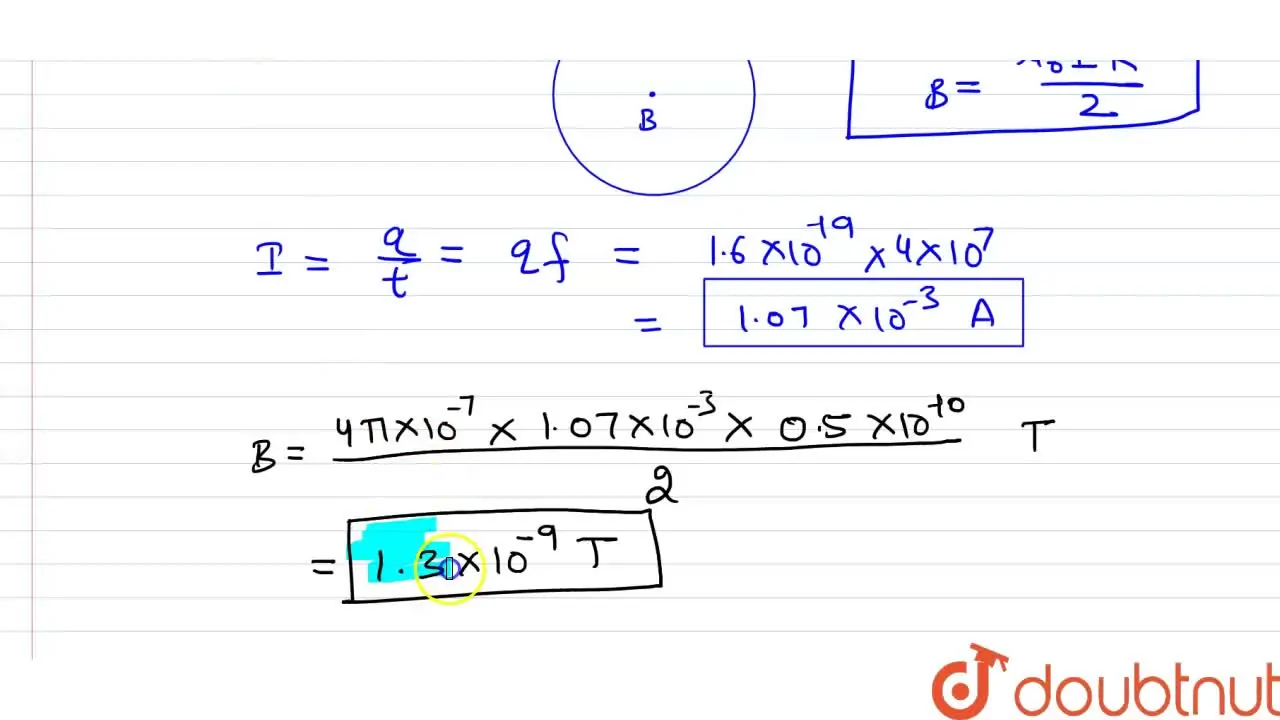
In a hydrogen atom the electron is making 4×107 revolution per minute in a path of radius 0.5 A∘. Find the magnetic field produced at the centre of orbit.
The electron due to its motion will produce current, so it can be assumed equivalent to a current carrying loop. Current produced due to electron motion
I=qf=1.6×10−19×4×10760=1.07×10−13
Field at centre
B=μ0I2R=4π×10−7×1.07×10−132×0.5×10−10=1.3×10−9T
Similar Questions
In hydrozen atom, the electron is making 6.6×1015 revolution per second in a circular path of radius 0.53A∘. What is the magnetic induction produced at the centre of the orbit?
View SolutionAn electron makes (3×105) revolutions per second in a circle of radius 0.5 angstrom. Find the magnetic field B at the centre of the circle.
View SolutionIn hydrogen atom, an electron is revolving in the orbit of radius 0.53Å with 6.6×1015rotations/second. Magnetic field produced at the centre of the orbit is
View SolutionIn hydrogen atom, the electron is making 6.6×1015rev/sec around the nucleus in an orbit of radius 0.528A. The magnetic moment (A-m^(2)) will be
View SolutionIn hydrogen atom, the electron is making 6.6×1015 rev/s around the nucleus in an orbit of radius 0.528∀. The magnetic moment is x×1023(Am)2. Find the value of x.
View SolutionIn hydrogen atom, the electron makes 6.6×1015 revolutions per second around the nucleus in an orbit of radius 0.5×10−10m. It is equivalent to a current nearly
View SolutionIn an hydrogen atom, the electron revolves around the nucleus in an orbit of radius 0.53×10−10m. Then the electrical potential produced by the nucleus at the position of the electron is
View SolutionA particle carrying a charge equal to 100 times the charge on an electron is rotating per second in a circular path of radius 0.8metre. The value of the magnetic field produced at the centre will be (μ0= permeability for vacuum)
View SolutionA particle having charge 100 times that of an electron is revolving in a circular path of radius 0.8m with one rotation per second. The magnetic field produced at the centre is
View SolutionIn an atom the electron has a time period of 0.16×10−15s in a circular orbit of radius 0.5A∘ .The magnetic induction at the centre of the orbit will be (in Tesla)
View Solution