A solid sphere A and a hollow sphere B have the same mass, radius and same angular velocity are moving in the same direction. The angular momentum of sphere A will be?
equal to B
less than B
more than B
insufficient data
The correct Answer is:B
To find the angular momentum of the solid sphere A, we will follow these steps:
Step 1: Understand the concept of angular momentum
Angular momentum (L) of a rotating object is given by the formula:
L=I⋅ω
where I is the moment of inertia and ω is the angular velocity.
Step 2: Identify the moment of inertia for both spheres
For a solid sphere, the moment of inertia IA is given by:
IA=25mr2
For a hollow sphere, the moment of inertia IB is given by:
IB=23mr2
Step 3: Substitute the values into the angular momentum formula
Since both spheres have the same mass m, radius r, and angular velocity ω, we can write the angular momentum for both spheres:
- For sphere A (solid sphere):
LA=IA⋅ω=(25mr2)⋅ω
- For sphere B (hollow sphere):
LB=IB⋅ω=(23mr2)⋅ω
Step 4: Compare the angular momentum of both spheres
We can compare the two angular momentum expressions:
- LA=25mr2⋅ω
- LB=23mr2⋅ω
Since 25<23, it follows that:
LA<LB
Conclusion
Thus, the angular momentum of sphere A (the solid sphere) will be less than that of sphere B (the hollow sphere).
Final Answer
The angular momentum of sphere A will be less than that of sphere B.
---
Angular momentum (L) of a rotating object is given by the formula:
L=I⋅ω
where I is the moment of inertia and ω is the angular velocity.
For a solid sphere, the moment of inertia IA is given by:
IA=25mr2
For a hollow sphere, the moment of inertia IB is given by:
IB=23mr2
Since both spheres have the same mass m, radius r, and angular velocity ω, we can write the angular momentum for both spheres:
- For sphere A (solid sphere):
LA=IA⋅ω=(25mr2)⋅ω
- For sphere B (hollow sphere):
LB=IB⋅ω=(23mr2)⋅ω
We can compare the two angular momentum expressions:
- LA=25mr2⋅ω
- LB=23mr2⋅ω
LA<LB
Thus, the angular momentum of sphere A (the solid sphere) will be less than that of sphere B (the hollow sphere).
The angular momentum of sphere A will be less than that of sphere B.
Similar Questions
A nollow sphere and a solid sphere having same mass and same radii are rolled down a rough incline plane.
View Solution
A solid sphere and a hollow sphere both of same mass and same radius are hit by a cue at a height h above the centre C. In which case,
(a). Linear velocity will be more?
(b). Angular velocity will be more?
(c). rotational kinetic energy will be more?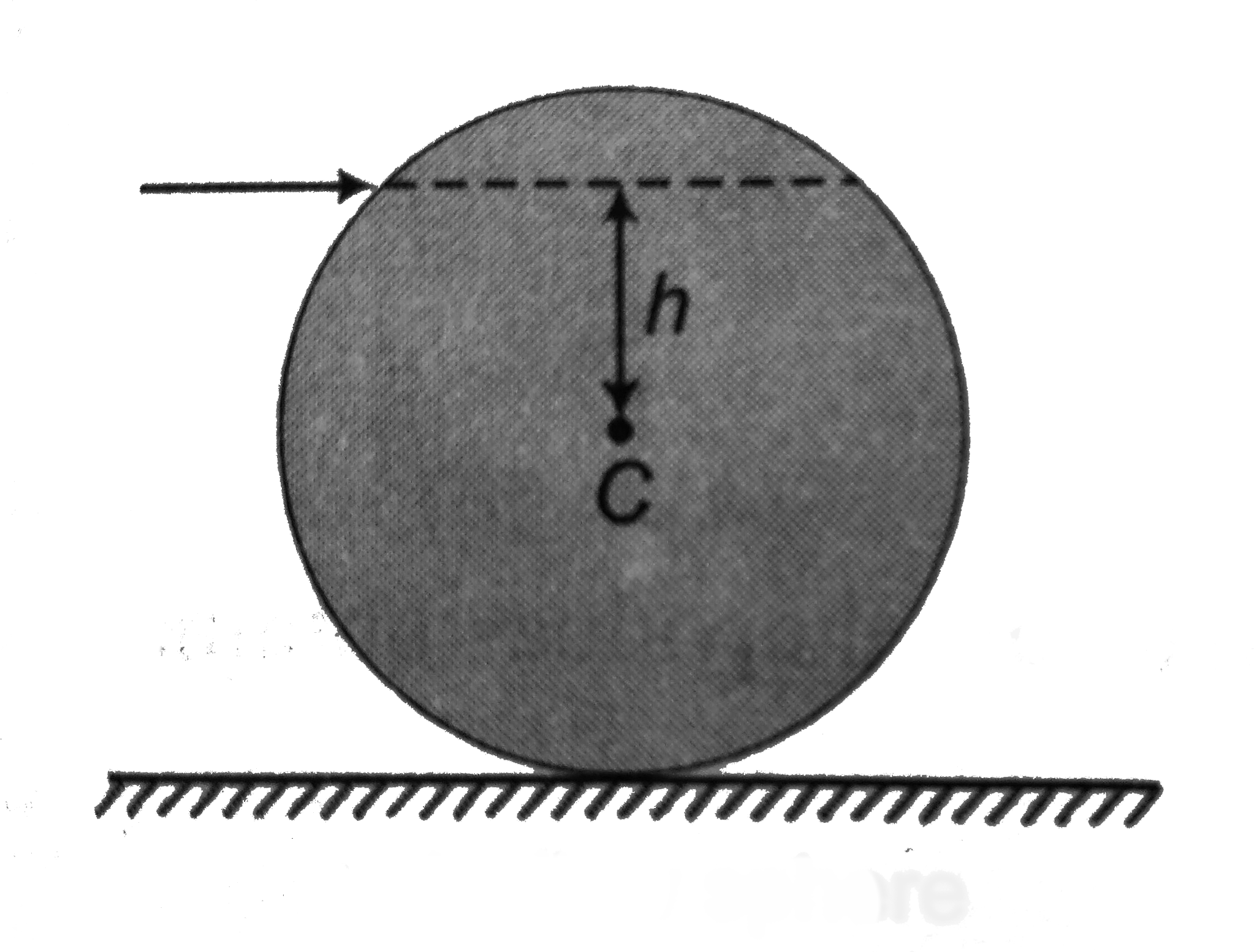
View Solution
Knowledge Check
If a solid and a hollow conducting sphere have same radius then
AHollow sphere will hold more maximum chargeBSolid sphere will hold more maximum chargeCBoth the spheres will hold same maximum chargeDBoth the sphere can't hold chargeA solid sphere and a hollow sphere are heated the same temperature . Point out the true statement.
Ahollow sphere cools more quicklyBboth hollow and solid sphere cools equallyCsolid sphere cools more quickly .Dnone of the statement is true.A solid sphere and a hollow sphere of the same material and of equal radii are heated to the same temperature.
ABoth will emit equal amount of radiation per unit time in the beginning.BBoth will absorb equal amount of radiation from the surrounding in the beginning.CThe initial rate of cooling (dTdt) will be the same for the two spheres.DThe two spheres will have equal temperature at any instant.
A solid sphere and a hollow sphere of the same material and of equal radii are heated to the same temperature
View SolutionA solid sphere and hollow sphere of the same material have mass. Then moment of inertia about the diameter is more for
View SolutionA ring and a solid sphere of same mass and radius are rotating with the same angular velocity about their diameteric axes then :-
View SolutionAssertion : A solid sphere and a hollow sphere of same material and same radius are kept at same temperature in atmosphere. Rate of cooling of hollow sphere will be more.
Reason : If all other conditions are same, then rate of cooling is inversely proportional to the mass of body.
View SolutionA hollow sphere and solid sphere of the same radius rotate about their diameters with the same angular velocity and angular momentum. Then the ratio of their masses is
View Solution
