A stick of length L and mass M lies on a frictionless horizontal surface on which it is free to move in any way. A ball of mass m moving with speed v collides elastically with the stick as shown in the figure. If after the collision the ball comes to rest, then what would be the mass of the ball?

m=2M
m=M
m=M/2
m=M/4
The correct Answer is:4
Applying the law of conservation of momentum mv=Mv…(i)By conservation of angular momentummv(L2)=(ML212)ω..(ii) As the collision Is elastic, we have 12mv2=12MV2+12ω2..(iii) or (Lω+V=ev where e=1)Subtituting the Values, we get m=M/4.
Similar Questions
A ball of mass m moving with velocity v collides head on elastically with another identical ball moving with velocity - V. After collision
View SolutionA meter stick of length l and mass M lies on a frictionlesss table. The stick is free to move in any way on the table. A hockey ball of mass m moving perpendicuarly to the mass of the ball so that it remains at rest immediately after the collision?
[Hint: Elastic collision means that kinetic energy is conserved in the process. Consider conservation of kinetic energy, conservation of angualr momentum and linear momentum, i.e., 12mv2 = (12Mv2'+12Iε2, mv12=Iε, mv=Mv′.
Eliminate v2' and w2 from the first with the help of the other two. Use the expression I=112MI2]
View Solution
Knowledge Check
A stick of length L and mass M lies on a frictionless horizontal surface on which it is free to move in any way. A ball of mass m moving with speed v collides elastically with the stick as shown in the figure. If after the collision the ball comes to rest, then what would be the mass of the ball?
 Am=2MBm=MCm=M/2Dm=M/4
Am=2MBm=MCm=M/2Dm=M/4A Stick of length L and mass M lies on a fnctionless horizontal surface on which it is free to move in any way. A ball of mass m moving with speed v collides elastically with the stick as shownin figure-5.115. If after the collision ball comes to rest, then what should be the mass of the ball ?
 Am=2MBm=MCm=M/2Dm=M/4
Am=2MBm=MCm=M/2Dm=M/4A ball of mass m moving with velocity v, collide with the wall elastically as shown in the figure. After impact the change in angular momentum about P is :
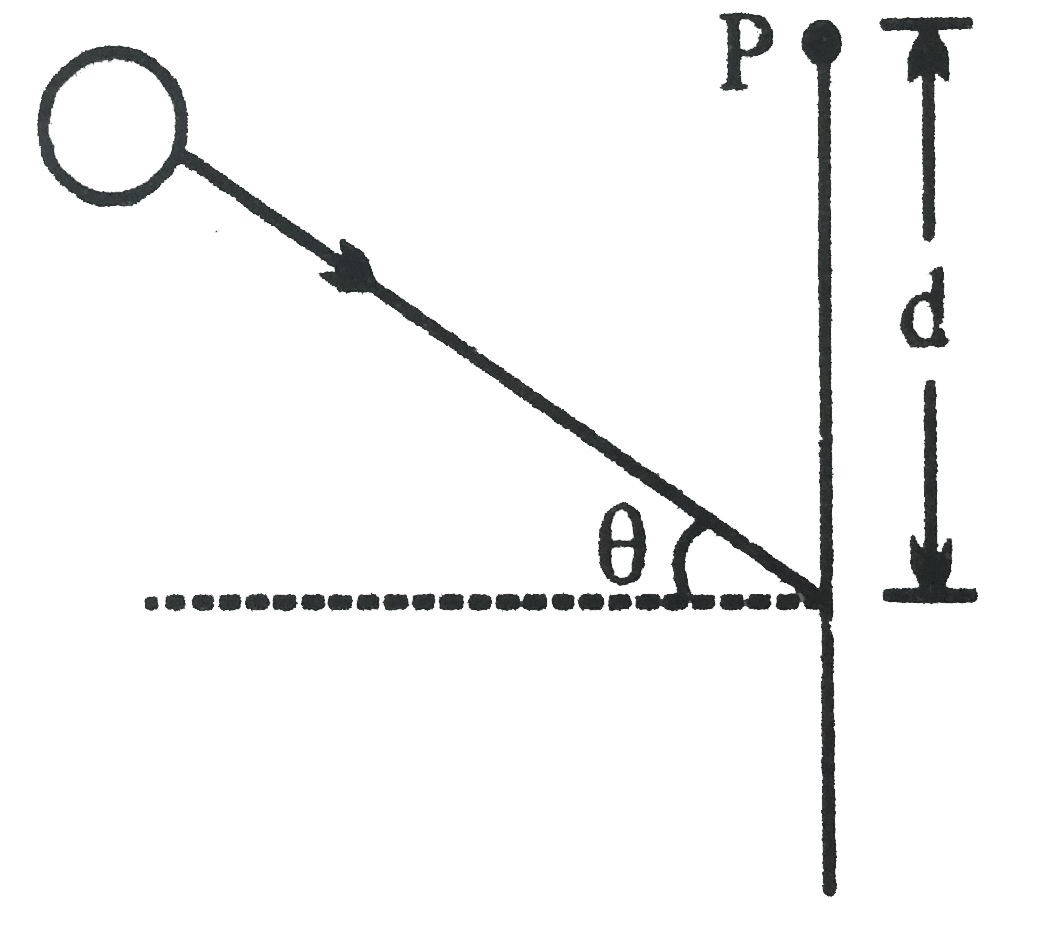 .A2mvdB2mvdcosθC2mvdsinθDzero
.A2mvdB2mvdcosθC2mvdsinθDzero
A body of a mass m moving with speed v collides elastically head on with another body of mass m, initially at rest. Show that the moving body will come to a stop after collision.
View Solution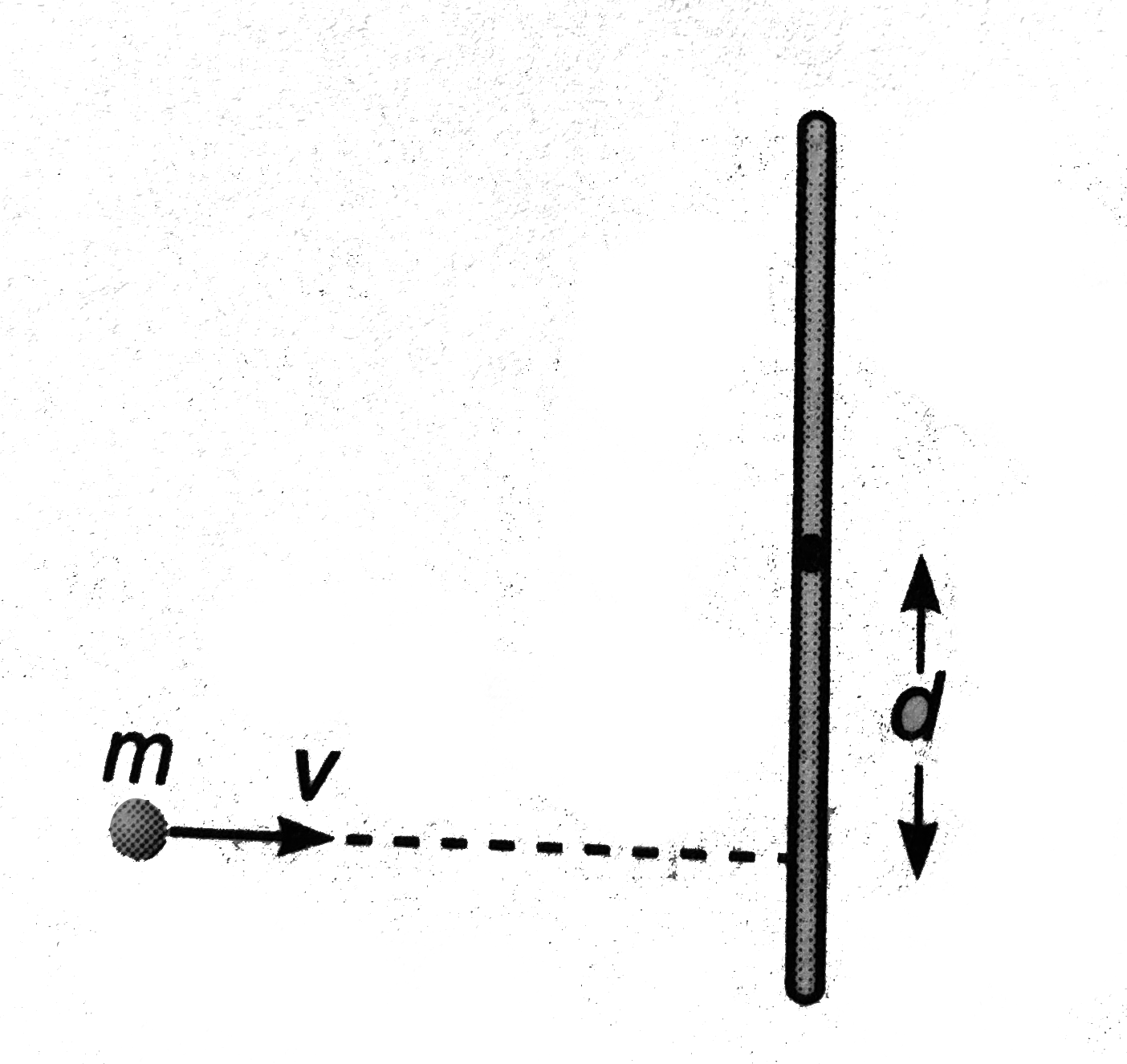
A stick of length l lies on horizontal table. It has a mass M and is free to move in any way on the table. A bal of mass m moving perpendicularly to the stick at a distance d from its centre with speed v collides elastically with it as shown in figure. what quantities are conserved in the collision ? what must be the mass of the ball, so that it remains at rest immediately after collision?
View SolutionA ball of mass 'm', moving with uniform speed, collides elastically with another stationary ball. The incident ball will lose maximum kinetic energy when the mass of the stationary ball is
View SolutionA ball of mass 'm', moving with uniform speed, collides elastically with another stationary ball. The incident ball will lose maximum kinetic energy when the mass of the stationary ball is
View SolutionA ball of mass M moving with speed v collides perfectly inelastically with another ball of mass m at rest. The magnitude of impulse imparted to the first ball is
View Solution