A disc rolls over a horizontal floor without slipping with a linear speed of 5 cm/sec. Then the linear speed of a particle on its rim, with respect to the floor, when it is in its highest position is?
10cm/sec
5cm/sec
2.5cm/sec
0
The correct Answer is:A
To find the linear speed of a particle on the rim of a disc when it is at its highest position while rolling without slipping, we can follow these steps:
Step 1: Understand the motion of the disc
The disc is rolling on a horizontal surface with a linear speed (V) of 5 cm/sec. In rolling motion, the center of mass of the disc moves forward, and all points on the disc have different velocities depending on their position relative to the center of mass.
Hint: Remember that in rolling motion, the speed of the center of mass is the same for all points on the disc, but rotational motion adds to the speed of points on the rim.
Step 2: Identify the point of interest
We are interested in the speed of a particle located at the highest point of the disc. At this position, the particle has both translational and rotational motion.
Hint: The highest point of the disc is where the particle is farthest from the center of mass in the upward direction.
Step 3: Calculate the translational speed
The translational speed (V) of the center of mass is given as 5 cm/sec. This speed applies to all points on the disc, including the highest point.
Hint: The translational speed is constant and equal to the speed of the center of mass.
Step 4: Calculate the rotational speed
For a point on the rim of the disc, the rotational speed (Vr) can be calculated using the relationship:
Vr=R⋅ω
where R is the radius of the disc and ω is the angular velocity.
Since the disc rolls without slipping, we have:
V=R⋅ω
Thus:
ω=VR
Hint: The angular velocity can be derived from the linear speed and radius of the disc.
Step 5: Find the total speed at the highest point
At the highest point, the total speed (Vp) of the particle is the sum of the translational speed and the rotational speed:
Vp=V+Vr
Since Vr=V (because at the highest point, the rotational speed adds to the translational speed):
Vp=V+V=2V
Step 6: Substitute the values
Substituting the value of V:
Vp=2×5cm/sec=10cm/sec
Conclusion
The linear speed of the particle on the rim of the disc at its highest position is 10 cm/sec.
---
The disc is rolling on a horizontal surface with a linear speed (V) of 5 cm/sec. In rolling motion, the center of mass of the disc moves forward, and all points on the disc have different velocities depending on their position relative to the center of mass.
We are interested in the speed of a particle located at the highest point of the disc. At this position, the particle has both translational and rotational motion.
The translational speed (V) of the center of mass is given as 5 cm/sec. This speed applies to all points on the disc, including the highest point.
For a point on the rim of the disc, the rotational speed (Vr) can be calculated using the relationship:
Vr=R⋅ω
where R is the radius of the disc and ω is the angular velocity.
V=R⋅ω
Thus:
ω=VR
At the highest point, the total speed (Vp) of the particle is the sum of the translational speed and the rotational speed:
Vp=V+Vr
Since Vr=V (because at the highest point, the rotational speed adds to the translational speed):
Vp=V+V=2V
Substituting the value of V:
Vp=2×5cm/sec=10cm/sec
The linear speed of the particle on the rim of the disc at its highest position is 10 cm/sec.
Similar Questions
A disc of radius 10 cm is rotating about its axis at an angular speed of 20 rad/s. Find the linear speed of
a. a point on the rim,
b. the middle point of a radius.
View SolutionA uniform ring rolls on a horizontal surface with out slipping. Its centre of mass moves with a constant speed v. then speed of the upper most point on its rim above the ground is
View Solution
Knowledge Check
A hoop rolls on a horizontal ground without slipping with linear speed v. Speed of a particle P on the circumference of the hoop at angle θ is :
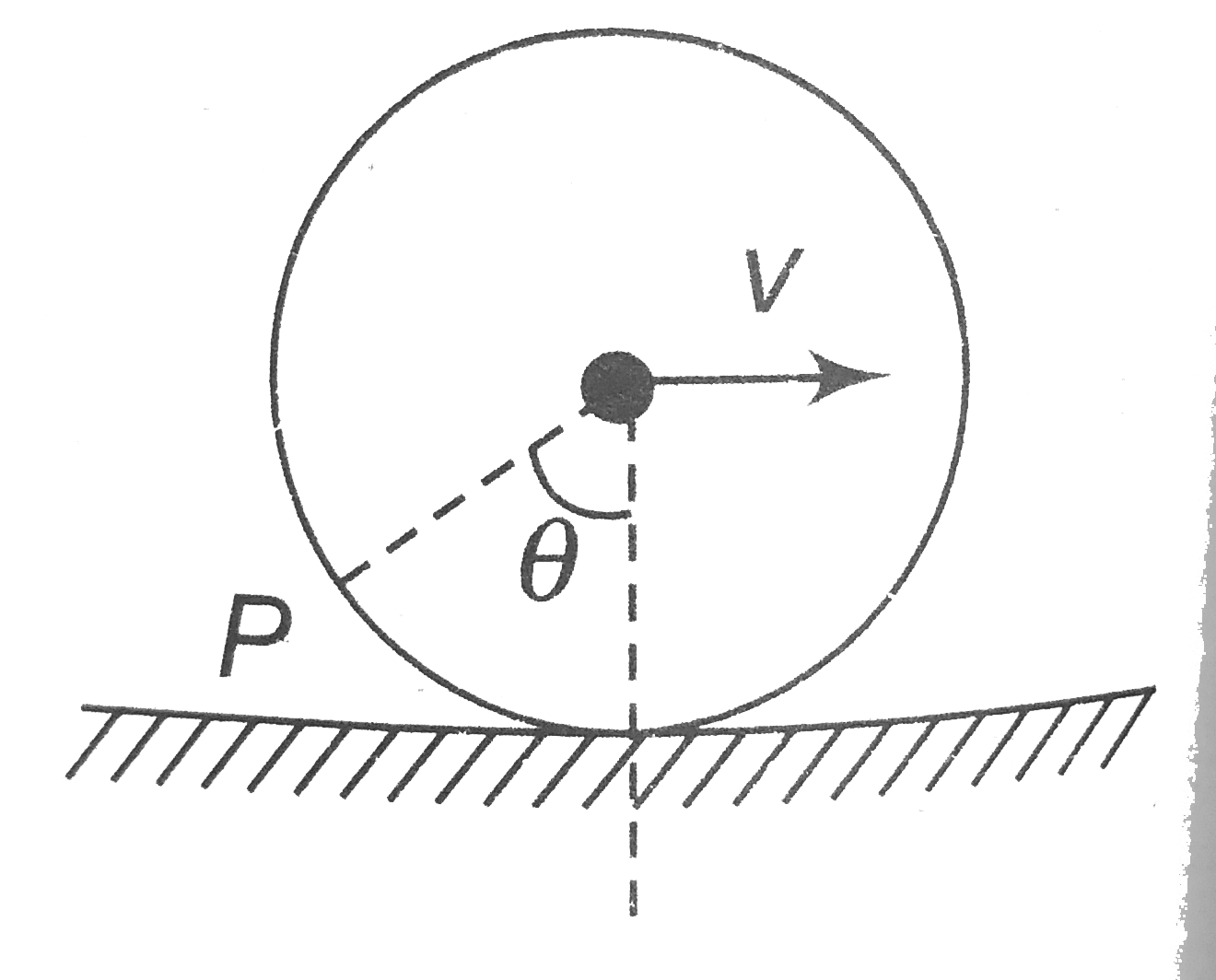 A2vsin(θ/2)BvsinθC2vcos(θ/2)Dvcosθ
A2vsin(θ/2)BvsinθC2vcos(θ/2)DvcosθAssertion: A disc rolls without slipping on a horizontal surface and the linear speed of its centre of mass is v. The rotational speed of the particles on its rim at the top of the disc will be 2v.
Reason: The disc rolls as if it is rotating about the point of contact with the horizontal surface.AAssertion is True, Reason is True, Reason is a correct explanation for AssertionBAssertion is True, Reason is True, Reason is not a correct explanation for AssertionCAssertion is False but, Reason is True.DAssertion is True, Reason is FalseA circular disc of mass 2 kg and radius 10 cm rolls without slipping with a speed 2 m/s. The total kinetic energy of disc is
A10 JB6 JC2 JD4 J
A ring and a disc roll on the horizontal surface without slipping with same linear velocity. If both have same mass and total kinetic energy of the ring is 4 J then total kinetic energy of the disc is
View SolutionA ring and a disc roll on the horizontal surface without slipping, with same linear velocity. If bolh have same mass and total kinetic energy of the ring is 4 J, then total kinetic energy of the disc is
View SolutionA ring and a disc roll on the horizontal surface without slipping with same linear velocity. If both have same mass and total kinetic energy of the ring is 4 J then total kinetic energy of the disc is
View SolutionA circular disc rolls on a horizontal floor without slipping and the center of the disc moves with a uniform velocity v. Which of the following values of the velocity at a point on the rim of the disc can have?
View SolutionA particle moves in a circular path of radius 0.5 m with a linear speed of 2 ms−1 ,its angular speed is
View Solution
