A hoop rolls on a horizontal ground without slipping with linear speed v. Speed of a particle P on the circumference of the hoop at angle θ is :
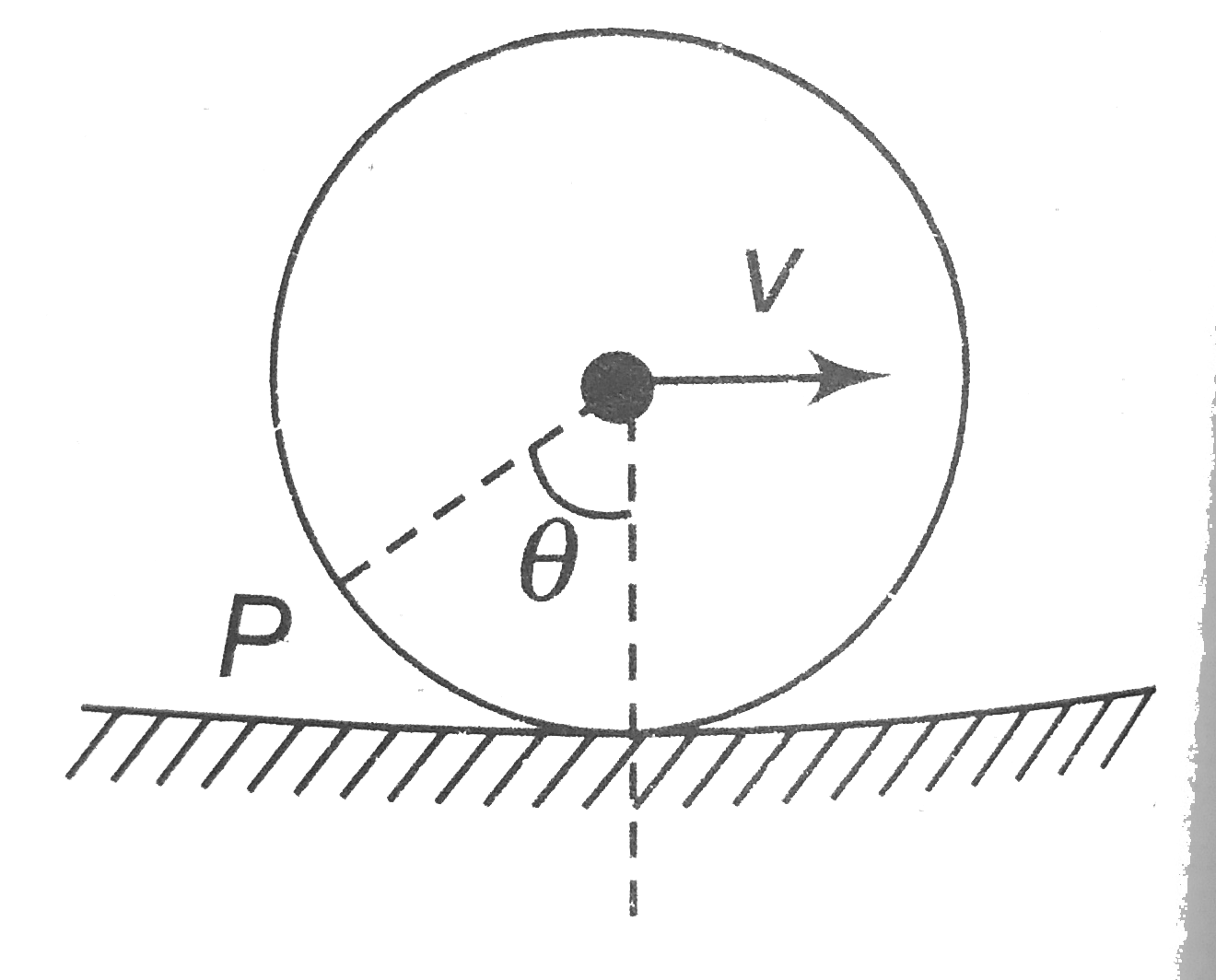
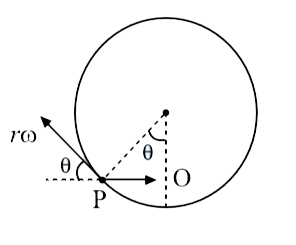
For rolling without slipping, VCM=rω The Velocity of P is the resultant of CM velocity and the tangential velocity rωdue to clockwise rotation velocity of )2=(VCM−rωcosθ)2+(rωsinθ)2=V2CM(1−cosθ)2+V2sin2θ(as rω=VCM=(4V2CMsin2)θ2⇒velocityofP=(2VCMsin)θ2.
Similar Questions
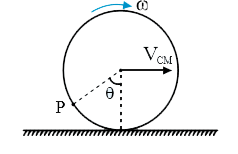
A disc rolls on ground without slipping . Velocity of centre of mass is v. There is a point P on circumference of disc at angle θ . Suppose vp is the speed of this point. Then, match the following the following table.

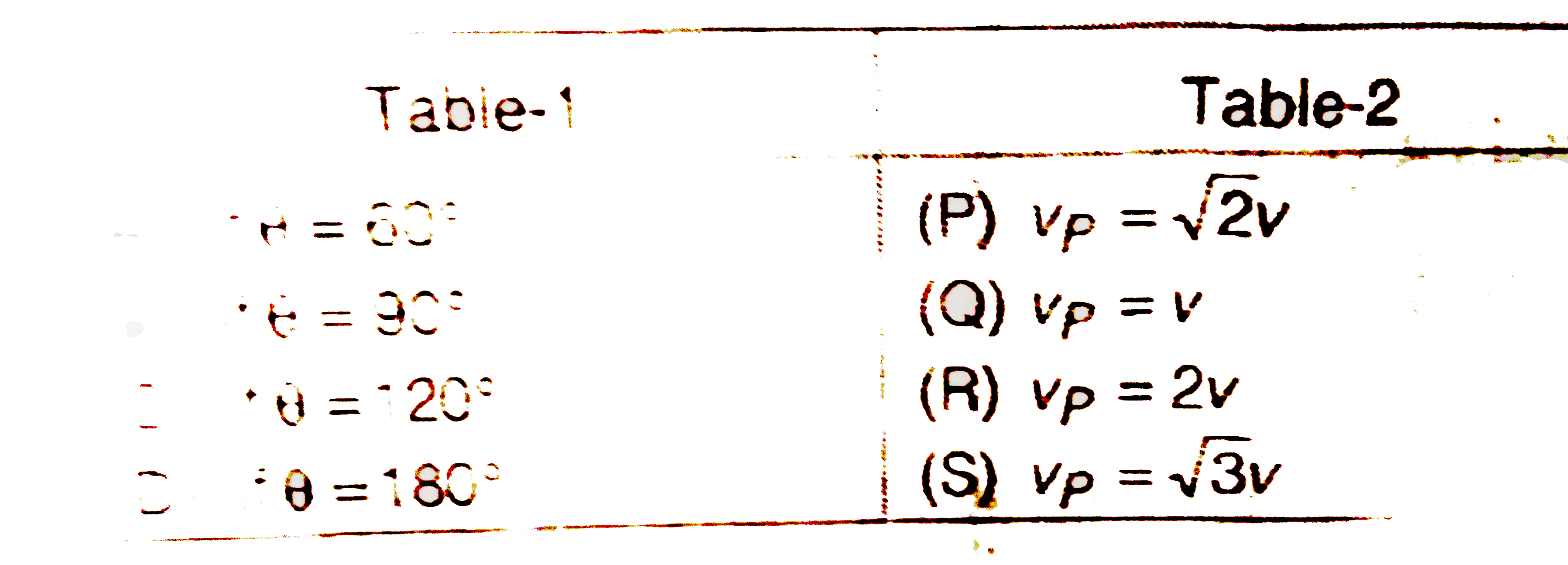
View SolutionA disc rolls on ground without slipping. Velocity of centre of mass is v. There is a point P on circumference of disc at angle θ. Suppose, vP is the speed of this point. Then, match the following columns
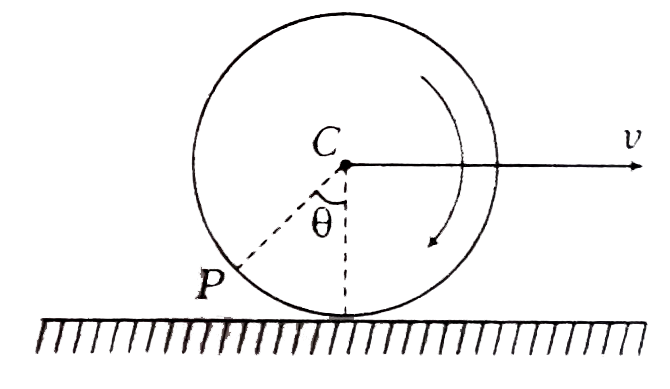
Column-IColumn-II(A)Ifθ=60∘(p)vP=√2v(B)Ifθ=90∘(q)vP=v(C)Ifθ=120∘(r)vP=2vD)Ifθ=180∘(s)vP=√3v
View Solution
Knowledge Check
A disc rolls over a horizontal floor without slipping with a linear speed of 5 cm/sec. Then the linear speed of a particle on its rim, with respect to the floor, when it is in its highest position is?
A10cm/secB5cm/secC2.5cm/secD0A smooth hoop lie as on a smooth horizontal table and is fixed. A particle is projected on the table form a point A on the inner circumference of the hoop at angle θ with radius vector . If e be the coefficient of restitution and the particle returns to the point of projection after two successive impacts. The final angle θ' made by velocity vector with radius of hoop is
 Atanθ'=e2(1+e2)tanθBtanθ'=e2tanθCtanθ'=tanθe2Dtanθ'=tanθe
Atanθ'=e2(1+e2)tanθBtanθ'=e2tanθCtanθ'=tanθe2Dtanθ'=tanθeA sphere of mass m and radius r rolls on a horizontal plane without slipping with a speed u. Now it rolls up vertically, then maximum height it would be attain will be
A3u24gB5u22gC7u210gDu22g
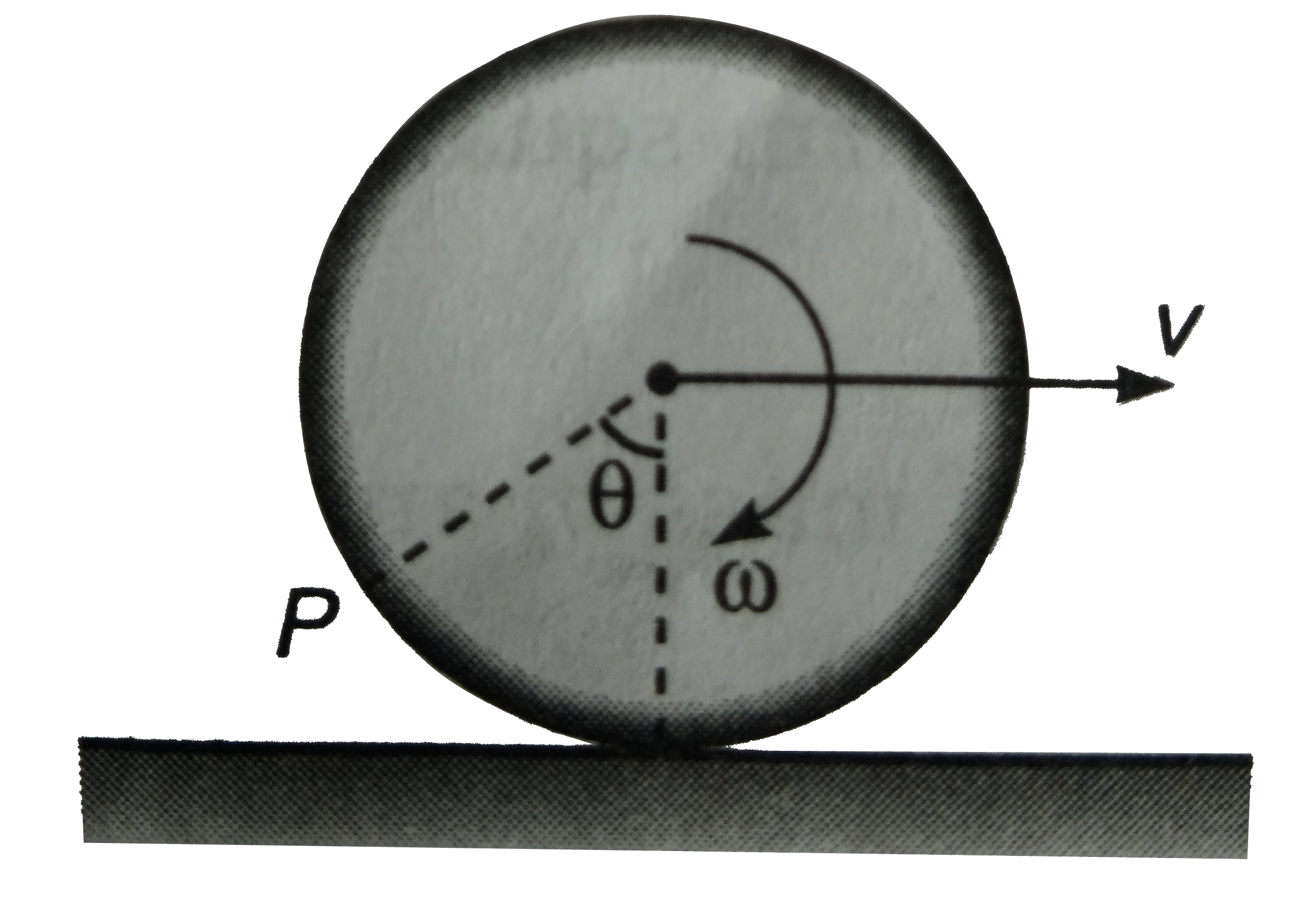
A ring of radius R rolls on a horizontal ground with linear speed v and angular speed ω. For what value of θ the velocity of point P is in vertical direction (v<Rω).
View SolutionA wheel is rolling straight on ground without slipping. If the axis of the wheel has speed v, the instantenous velocity of a point P on the rim, defined by angle θ, relative to the ground will be

View SolutionThe centre of a wheel rolling without slipping on a plane surface moves with a speed v0. A particle on the rim of the wheel at the same level as the centre of wheel will be moving with speed
View SolutionA sphere of mass m and radius r rolls on a horizontal plane without slipping with the speed u . Now if it rolls up vertically , the maximum height it would attain will be
View SolutionA uniform ring rolls on a horizontal surface with out slipping. Its centre of mass moves with a constant speed v. then speed of the upper most point on its rim above the ground is
View Solution
