The radius of gyration of a solid shapere of radius r about a certain axis is r. The distance of this axis from the centre of the shpere is
Video Solution
Text Solution
I=ICM+Md2 (parallel axis therorem) Mk2=25MR2+Md2 (But k+R) ⇒MR2=25MR2+Md2⇒d=√0.6R.
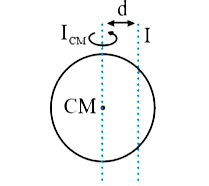
|
Similar Questions
Knowledge Check
The radius of gyration of a solid sphere of radius r about a certain axis is r. The distance of this axis from the centre of the sphere is
ArB0.5 rC√0.6rD√0.4rThe radius of gyration of a solid sphere of radius R about its tangential is
A√75RB√25RC√57DRThe radius of gyration of a sphere of radius R about a tangent is.
A√23RB√25RC√53RD√75R
The radius of gyration of a solid sphere of radius R about a certain axis is also equal to R. If r is the distance between the axis and the centre of the sphere, then r is equal to
View SolutionThe radius of gyration of a solid cylinder of mass M and radius R about its own axis is
View SolutionThe radius of gyration of a disc of radius 25 cm about a centroidal axis perpendicular to disc is
View SolutionThe radius of gyration of a uniform disc of radius R, about an axis passing through a point R2 away from the centre of disc, and perpendicular to the plane of disc is:
View SolutionThe radius of gyration of a uniform disc of radius R, about an axis passing through a point R2 away from the centre of disc, and perpendicular to the plane of disc is:
View Solution
