A particle is projected vertically upward with initial velocity 25 ms–1. During third second of its motion, which of the following statement is correct ?
displacement of the particle is 30 m
distance covered by the particle is 30 m
distance covered by the particle is 2.5 m
None of these
To solve the problem, we need to determine the distance covered by a particle projected vertically upwards with an initial velocity of 25 m/s during the third second of its motion.
1. Understanding the Motion:
The particle is projected upwards with an initial velocity u=25m/s. The acceleration due to gravity g acts downwards and is approximately 10m/s2.
2. Determine the Time Intervals:
We need to find the distance covered during the third second. The third second refers to the time interval from t=2s to t=3s.
3. Calculate the Displacement at t=3s:
The displacement s after time t can be calculated using the formula:
s=ut+12(−g)t2
For t=3s:
s(3)=25×3−12×10×(32)
s(3)=75−12×10×9
s(3)=75−45=30m
4. Calculate the Displacement at t=2s:
Now, calculate the displacement at t=2s:
s(2)=25×2−12×10×(22)
s(2)=50−12×10×4
s(2)=50−20=30m
5. Calculate the Distance Covered During the Third Second:
The distance covered during the third second is given by:
Distance covered=s(3)−s(2)
Distance covered=30m−30m=0m
However, we need to calculate the distance traveled in the interval from t=2s to t=3s.
6. Calculate the Distance Traveled:
The particle reaches its maximum height and then starts descending. We need to calculate the distance traveled in the third second:
- The distance covered in the upward motion from t=2s to t=3s is:
Distance=Upward distance−Downward distance
- Upward distance from t=2 to t=2.5:
s(2.5)=25×2.5−12×10×(2.52)
s(2.5)=62.5−31.25=31.25m
- Downward distance from t=2.5 to t=3:
s(3)=30m
- Thus, the distance covered in the third second is:
Distance=s(3)−s(2.5)=31.25−30=1.25m
- Therefore, the total distance covered in the third second is:
Distance=2.5m
Conclusion:
The correct statement is that the distance covered by the particle during the third second is 2.5 m.
The particle is projected upwards with an initial velocity u=25m/s. The acceleration due to gravity g acts downwards and is approximately 10m/s2.
We need to find the distance covered during the third second. The third second refers to the time interval from t=2s to t=3s.
The displacement s after time t can be calculated using the formula:
s=ut+12(−g)t2
For t=3s:
s(3)=25×3−12×10×(32)
s(3)=75−12×10×9
s(3)=75−45=30m
Now, calculate the displacement at t=2s:
s(2)=25×2−12×10×(22)
s(2)=50−12×10×4
s(2)=50−20=30m
The distance covered during the third second is given by:
Distance covered=s(3)−s(2)
Distance covered=30m−30m=0m
However, we need to calculate the distance traveled in the interval from t=2s to t=3s.
The particle reaches its maximum height and then starts descending. We need to calculate the distance traveled in the third second:
- The distance covered in the upward motion from t=2s to t=3s is:
Distance=Upward distance−Downward distance
- Upward distance from t=2 to t=2.5:
s(2.5)=25×2.5−12×10×(2.52)
s(2.5)=62.5−31.25=31.25m
- Downward distance from t=2.5 to t=3:
s(3)=30m
- Thus, the distance covered in the third second is:
Distance=s(3)−s(2.5)=31.25−30=1.25m
- Therefore, the total distance covered in the third second is:
Distance=2.5m
The correct statement is that the distance covered by the particle during the third second is 2.5 m.
Similar Questions
Knowledge Check
A particle is projected vertically upward with velocity u from a point A, when it returns to the point of projection .
AIts average speed is u/2.BIts average velocity is zero.CIts displacement is zero.DIts average speed is u.A particle is thrown vertically upwards with a velocity v. It returns to the ground in time T. which of the following graphs correctly represents the motion ?
A B
B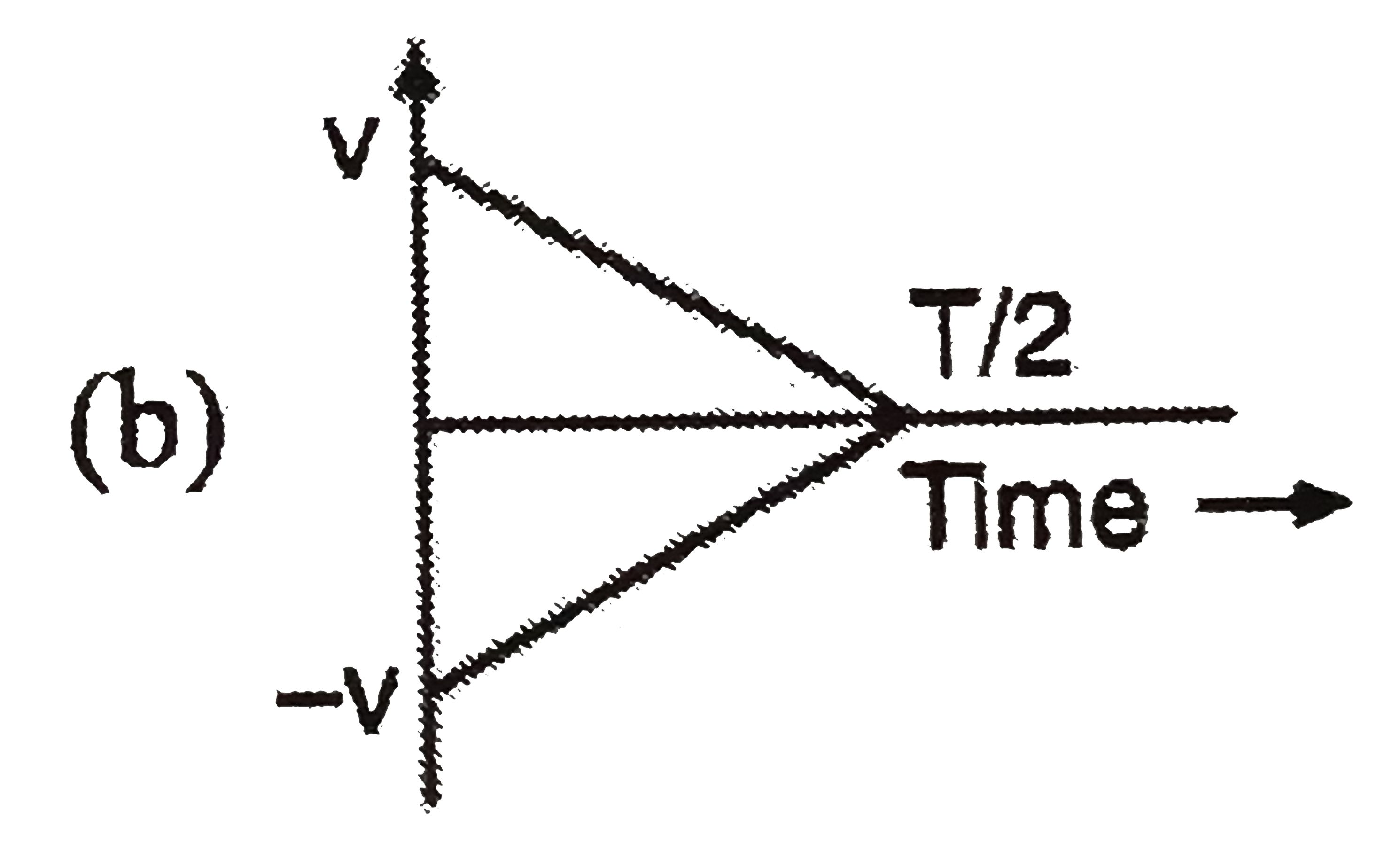 C
C D
D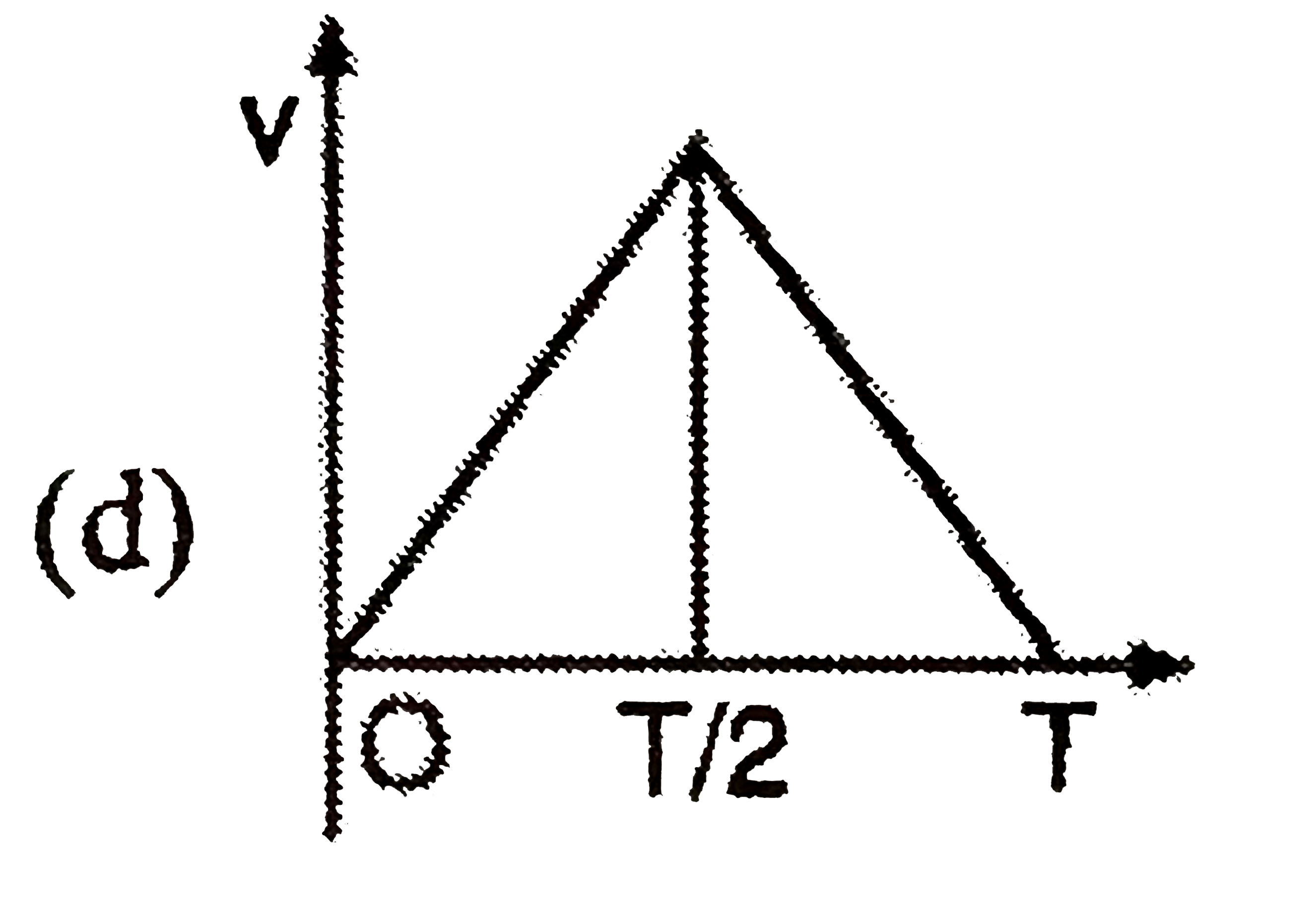
A particle is projected vertically upward and is at a height h after t1 seconds and again after t2 seconds
Ah=gt1t2Bh=12gt1t2Ch=2gt1t2Dh=√gt1t2
A particle is projected vertically upwards from ground with velocity 10 m/s. Find the time taken by it to reach at the highest point ?
View SolutionA particle is parojected vertically upwards from grund with initial velocity u.
a. Find the maximum height H the particle will attain and time T that it will attain and time T that it will take to return to the ground .
 .
.
b. What is the velocity when the particle returns to the ground?
c. What is the displacement and distance travelled by the particle during this time of whole motion.
View SolutionA particle is projected vertically upwards with an initial velocity of 40m/s. Find the displacement and distance covered by the particle in 6s. Take g=10m/s2.
View SolutionA stone is dropped from a height of 100m .At the same instant another stone is projected vertically upwards with velocity of 50ms^(-1) .If g=10ms^(-2) ,the height from the ground at which the 2 stones meet is
View SolutionA particle is projected vertically upwards and it reaches the maximum height H in time T seconds. The height of the particle at any time t will be-
View Solution
