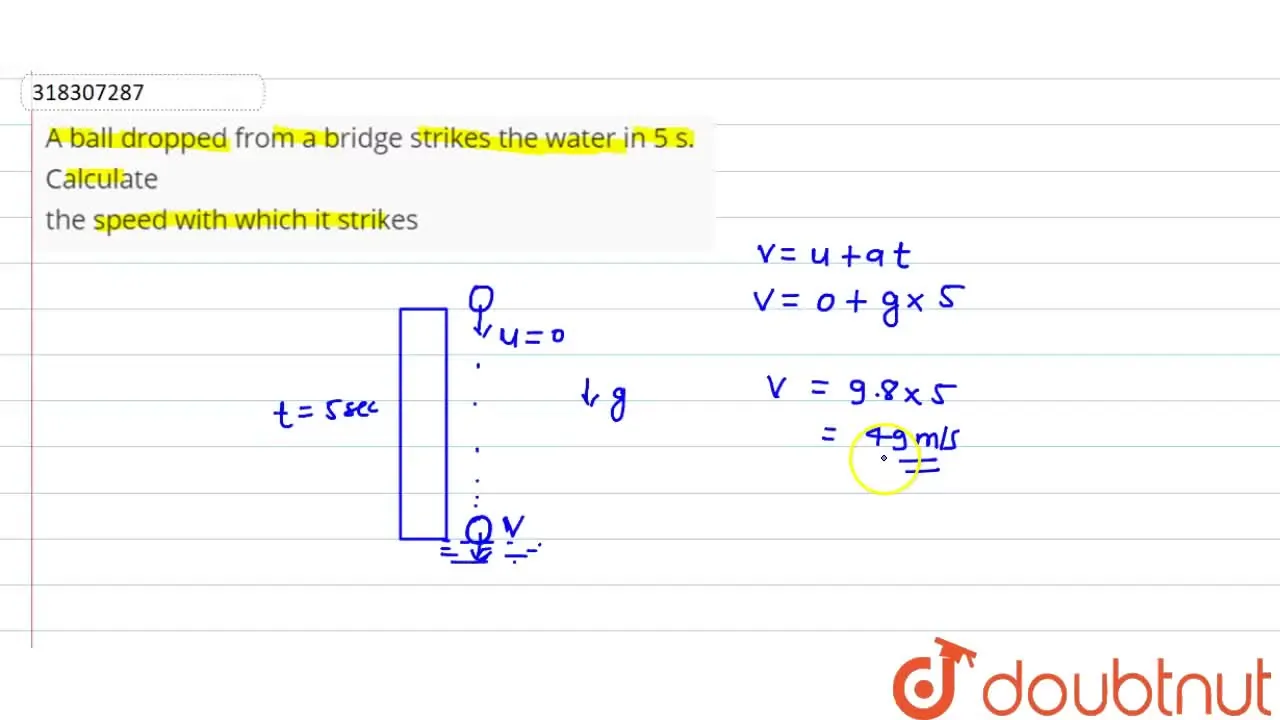
A ball dropped from a bridge strikes the water in 5 s. Calculate
the speed with which it strikes

Video Solution

Text Solution

Generated By DoubtnutGPT

To solve the problem of a ball dropped from a bridge that strikes the water in 5 seconds, we can use the equations of motion under uniform acceleration due to gravity.
1. Identify the Given Information:
- Time of fall (t) = 5 seconds
- Initial velocity (u) = 0 m/s (since the ball is dropped)
- Acceleration due to gravity (g) = 9.81 m/s² (approximately)
2. Use the Equation of Motion:
We can use the equation of motion that relates final velocity (v), initial velocity (u), acceleration (a), and time (t):
$v = u + a t$
Here, since the ball is dropped, the initial velocity $u = 0$ .
3. Substitute the Values:
Substitute the known values into the equation:
$v = 0 + (9.81 {m/s}^{2}) (5 s)$
4. Calculate the Final Velocity:
$v = 9.81 \times 5 = 49.05 m/s$
5. Conclusion:
The speed with which the ball strikes the water is approximately 49.05 m/s.

Updated on:18/9/2024

A ball is dropped vertically from a height of h onto a hard surface. If the ball rebounds from the surface with a fraction r of the speed with which it strikes the latter on each impact, what is the net distance traveled by the ball up to the $10^{t h}$ impact ?
A $2 h \frac{1 - r^{10}}{1 - r}$
B $h \frac{1 - r^{20}}{1 - r^{2}}$
C $2 h \frac{1 - r^{22}}{1 - r^{2}} - h$
D $2 h \frac{1 - r^{20}}{1 - r^{2}} - h$
A bomber plane moves horizontally with a speed of $600 m / s$ and a bomb released from it, strikes the ground in $10 s$ . The angle with horizontally at which it strikes the ground will be
A ${tan}^{- 1} (1 / 2)$
B ${tan}^{- 1} (1 / 6)$
C ${tan}^{- 1} (4 / 5)$
D ${tan}^{- 1} (3 / 4)$
From the top of the tower, a ball $A$ is dropped and another ball $B$ is thrown horizontally at the same time. Which ball strikes the ground first ?
A $A$
B $B$
Csimultaneously
Ddepends on the masses