The length of a vertical pole at the surface of a lake of water (μ=43) is 24 cm. Then to an under-water fish just below the water surface the tip of the pole appeard to be
18 cm above the surface
24 cm above the surface
32 cm above the surface
36 cm above the surface
The correct Answer is:C
To solve the problem, we need to find the apparent height of the vertical pole as seen by a fish just below the water surface. The actual height of the pole is given as 24 cm, and the refractive index of water is given as μ=43.
1. Understanding the Concept of Apparent Height:
The apparent height of an object when viewed from a different medium (in this case, from water to air) is less than its actual height due to the refraction of light. The relationship between the apparent height (h') and the actual height (h) can be expressed using the refractive index (μ):
h′h=1μ
2. Substituting the Known Values:
Here, the actual height h=24 cm, and the refractive index μ=43. We can substitute these values into the equation:
h′24=143
3. Calculating the Apparent Height:
Rearranging the equation to find h′:
h′=24×143=24×34
Simplifying this gives:
h′=24×0.75=18 cm
4. Conclusion:
Therefore, the apparent height of the tip of the pole as seen by the fish just below the water surface is 18 cm.
Final Answer:
The tip of the pole appears to be 18 cm above the water surface to the underwater fish.
The apparent height of an object when viewed from a different medium (in this case, from water to air) is less than its actual height due to the refraction of light. The relationship between the apparent height (h') and the actual height (h) can be expressed using the refractive index (μ):
h′h=1μ
Here, the actual height h=24 cm, and the refractive index μ=43. We can substitute these values into the equation:
h′24=143
Rearranging the equation to find h′:
h′=24×143=24×34
Simplifying this gives:
h′=24×0.75=18 cm
Therefore, the apparent height of the tip of the pole as seen by the fish just below the water surface is 18 cm.
The tip of the pole appears to be 18 cm above the water surface to the underwater fish.
Topper's Solved these Questions
- RAY OPTICS AND OPTICAL INSTRUMENTSBook:AAKASH INSTITUTEChapter:RAY OPTICS AND OPTICAL INSTRUMENTSExercise:ASSIGNMENT (SECTION - B)
Explore 30 Videos
- RAY OPTICS AND OPTICAL INSTRUMENTSBook:AAKASH INSTITUTEChapter:RAY OPTICS AND OPTICAL INSTRUMENTSExercise:ASSIGNMENT (SECTION - C)
Explore 76 Videos
- RAY OPTICS AND OPTICAL INSTRUMENTSBook:AAKASH INSTITUTEChapter:RAY OPTICS AND OPTICAL INSTRUMENTSExercise:EXERCISE
Explore 47 Videos
- PHYSICAL WORLDBook:AAKASH INSTITUTEChapter:PHYSICAL WORLDExercise:ASSIGNMENT (Section-B)
Explore 5 Videos
- SEMICONDUCTOR ELECTRONICS (MATERIAL, DEVICES AND SIMPLE CIRUITS )Book:AAKASH INSTITUTEChapter:SEMICONDUCTOR ELECTRONICS (MATERIAL, DEVICES AND SIMPLE CIRUITS )Exercise:Assignment SECTION - D (Assertion & reason type Question)
Explore 10 Videos
Similar Questions
_E01_107_Q01.png)
Two very wide parallel glass plates are held vertically at a small separation d, and dipped in water. Some water climbs up in the gap between the plate. Let S be the surface tension of water P0= atmospheric pressure, P= pressure of water just below the water surface in the region between the plates-
View SolutionWhen an air bubble rise from the bottom of a deep lake to a point just below the water surface, the pressure of air inside the bubble
View Solution
Knowledge Check
Temperature of water at the surface of lake is −20∘C. Then temperature of water just below the lower surface of ice layer is
A−4∘CB0∘CC4∘CD−20∘CA bird is flying 3m above the surface of water. To a fish underwater, the height of the bird from the water surface appears to be
A2.25mB3.33mC4mD4/3mA man looks down on a fish of length 20 cm. His eye is 2m above the surface of the water (μ=4/3) and the fish is 2m below the surface as shown in the figure the ratio of angular width Δθ of the fish as seen by the man in presence of water to the Δθ in the absence of water is (Δθ is small)
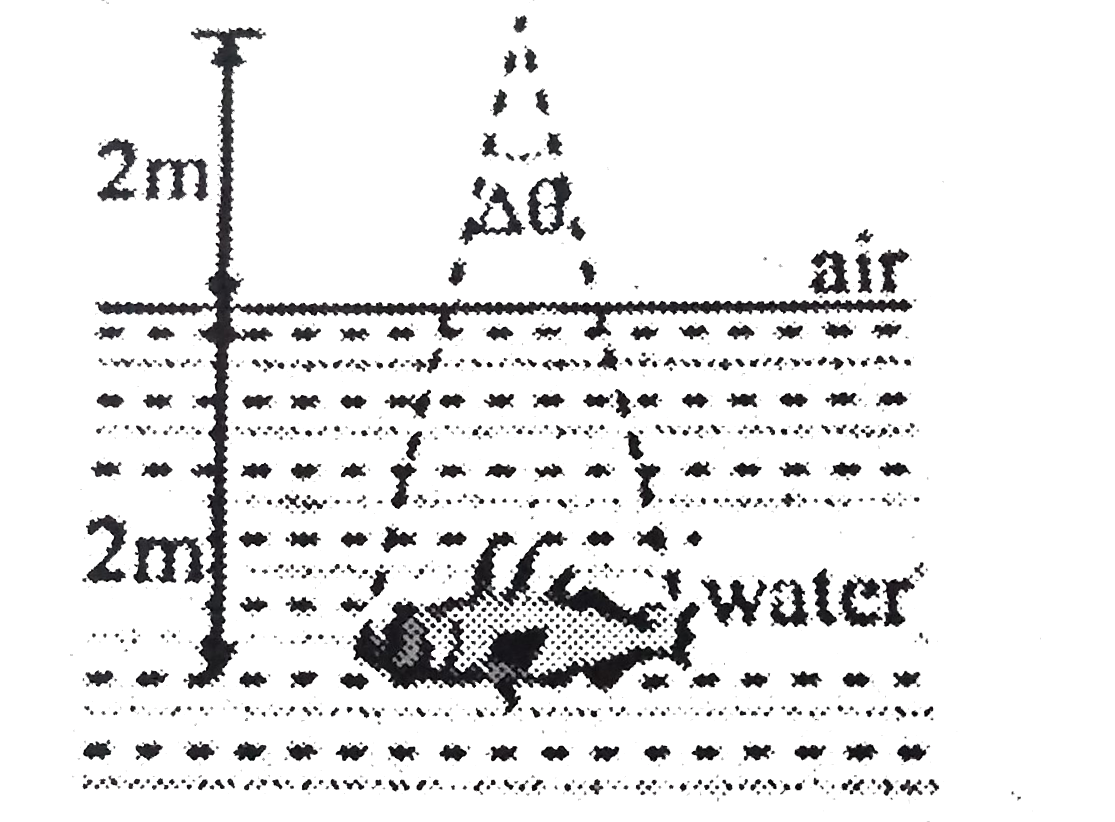 A65B5/6C7/8D8/7
A65B5/6C7/8D8/7
A bird in air looks at a fish vertically below it and inside water. h1 is the height of the bird above the surface of water and h2, the depth of the fish below the surface of water. If refractive index of water with respect to air be μ, then the distance of the fish as observed by the bird is
View SolutionA fish is a little away below the surface of a lake. If the critical angle is 49∘ , then the fish could see things above the water surface with in an angular range of θ∘ where

View SolutionThe length of needle foating on the surface of water is 1.5 cm the force in addition to its weight required to lift the needle from water surface will be (surface tension of water =7.5N/cm)
View SolutionIn a pond of water, a flame is held 2 m above the surface of the water. A fish is at depth of 4 m from the water surface. Refractive index of water is 43. The apparent height of the flame from the eyes of fish is -
View SolutionA capillary tube is kept vertical with the lower end dipped in water . The height of water raised in the capillary is 4 cm . If the length of the capillary tube is made 2 cm , then the angle made by the water surface in the capillary with the wall is
View Solution