For a concave mirror, paraxial rays are focused at distance R2 from pole and marginal rays are focused at distance x from pole, then (R is radius of curvature)
x=R2
x=−f
x>R2
x<R2
The correct Answer is:D
To solve the problem, we need to understand the behavior of paraxial rays and marginal rays in a concave mirror.
1. Understanding Paraxial Rays:
- Paraxial rays are those rays that are close to the principal axis of the mirror. For a concave mirror, these rays converge at the focal point, which is located at a distance of R2 from the pole of the mirror, where R is the radius of curvature.
2. Understanding Marginal Rays:
- Marginal rays are those rays that are further away from the principal axis. They make a larger angle with the normal at the point of incidence on the mirror. These rays also converge to a point, but this point is different from the focal point for paraxial rays.
3. Setting Up the Geometry:
- Consider a concave mirror with its pole (P) and center of curvature (C). The focal point (F) for paraxial rays is at R2 from the pole.
- For marginal rays, we need to analyze the geometry involving the angles formed by these rays.
4. Using Trigonometry:
- For marginal rays, the angle of incidence is larger than 10∘. We denote this angle as θ.
- The distance from the center of curvature to the point where the marginal rays focus can be expressed in terms of θ.
5. Finding the Distance x:
- The distance x from the pole to the focus of the marginal rays can be derived using the cosine of the angle θ:
CE=R2cos(θ)
- The distance from the center of curvature to the pole is R, so the distance from the pole to the focus of the marginal rays can be expressed as:
x=R−CE=R−R2cos(θ)=R(1−12cos(θ))
6. Conclusion:
- As θ increases, cos(θ) decreases, which means x will be less than R2. Therefore, the focus for marginal rays will be less than R2.
Final Answer:
The distance x from the pole to the focus of the marginal rays is given by:
x=R(1−12cos(θ))
where x<R2.
- Paraxial rays are those rays that are close to the principal axis of the mirror. For a concave mirror, these rays converge at the focal point, which is located at a distance of R2 from the pole of the mirror, where R is the radius of curvature.
- Marginal rays are those rays that are further away from the principal axis. They make a larger angle with the normal at the point of incidence on the mirror. These rays also converge to a point, but this point is different from the focal point for paraxial rays.
- Consider a concave mirror with its pole (P) and center of curvature (C). The focal point (F) for paraxial rays is at R2 from the pole.
- For marginal rays, we need to analyze the geometry involving the angles formed by these rays.
- For marginal rays, the angle of incidence is larger than 10∘. We denote this angle as θ.
- The distance from the center of curvature to the point where the marginal rays focus can be expressed in terms of θ.
- The distance x from the pole to the focus of the marginal rays can be derived using the cosine of the angle θ:
CE=R2cos(θ)
- The distance from the center of curvature to the pole is R, so the distance from the pole to the focus of the marginal rays can be expressed as:
x=R−CE=R−R2cos(θ)=R(1−12cos(θ))
- As θ increases, cos(θ) decreases, which means x will be less than R2. Therefore, the focus for marginal rays will be less than R2.
The distance x from the pole to the focus of the marginal rays is given by:
x=R(1−12cos(θ))
where x<R2.
Topper's Solved these Questions
- RAY OPTICS AND OPTICAL INSTRUMENTSBook:AAKASH INSTITUTEChapter:RAY OPTICS AND OPTICAL INSTRUMENTSExercise:ASSIGNMENT (SECTION - A)
Explore 42 Videos
- RAY OPTICS AND OPTICAL INSTRUMENTSBook:AAKASH INSTITUTEChapter:RAY OPTICS AND OPTICAL INSTRUMENTSExercise:ASSIGNMENT (SECTION - B)
Explore 30 Videos
- RAY OPTICS AND OPTICAL INSTRUMENTSBook:AAKASH INSTITUTEChapter:RAY OPTICS AND OPTICAL INSTRUMENTSExercise:EXAMPLE
Explore 75 Videos
- PHYSICAL WORLDBook:AAKASH INSTITUTEChapter:PHYSICAL WORLDExercise:ASSIGNMENT (Section-B)
Explore 5 Videos
- SEMICONDUCTOR ELECTRONICS (MATERIAL, DEVICES AND SIMPLE CIRUITS )Book:AAKASH INSTITUTEChapter:SEMICONDUCTOR ELECTRONICS (MATERIAL, DEVICES AND SIMPLE CIRUITS )Exercise:Assignment SECTION - D (Assertion & reason type Question)
Explore 10 Videos
Similar Questions
Knowledge Check
An object is at a distance of 10 cm from a concave mirror and the image of the object is at a distance of 30 cm from the mirror on the same side as that of the object. The radius of curvature of the concave mirror is
A+15.0 cmB+7.5 cmC−7.5 cmD−15.0 cmA transparent thin film of uniform thickness and refractive index n1=1.4 is coated on the convex spherical surface of radius R at one end of a long solid glass cylinder of refractive index n2=1.5, as shown in the figure. Rays of light parallel to the axis of the cylinder traversing through the film from air to glass get focused at distance f1 from the film, while rays of light traversing from glass to air get focused at distance f2 from the film, Then
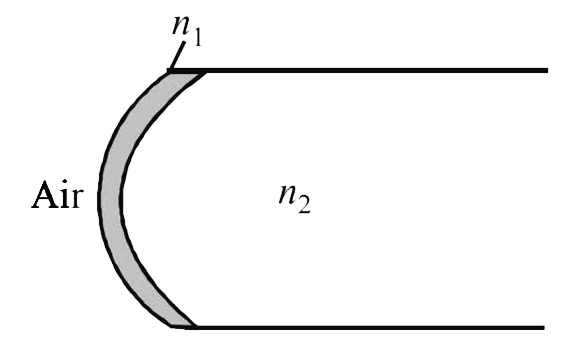 A|f1|=3RB|f1|=2.8RC|f2|=1.4RD|f2|=5.4R
A|f1|=3RB|f1|=2.8RC|f2|=1.4RD|f2|=5.4RAn object placed in front of a concave mirror at a distance of x cm from the pole gives a 3 times magnified real image. If it is moved to a distance of (x+5) cm, the magnification of the image becomes 2. The focal length of the mirror is
A15 cmB20 cmC25 cmD30 cm
An object is placed at a distance of 15 cm from a convex mirror and images is formed at a distance of 5 cm from the mirror. Calculate the radius of curvature of the mirror.
View SolutionAn object is placed beyond the centre of curvature C of the given concave mirror . If the distance of the object is d1 from C and the distance of the image formed is d2 from C , the radius of curvature of this mirror is
View SolutionThe figure ,shows a transparent sphere of radiusRand refractive indexμ.An object Ois placed at a distance x from the pole of the first surface so that a real image is formed at the pole of the exactly opposite surface.
 if an object is Placed at a distanceR from the pole of first surface ,then the real image is formed at a distance Rfrom thepole of the second surface.The refractive indexμ of the spher is given by
if an object is Placed at a distanceR from the pole of first surface ,then the real image is formed at a distance Rfrom thepole of the second surface.The refractive indexμ of the spher is given by
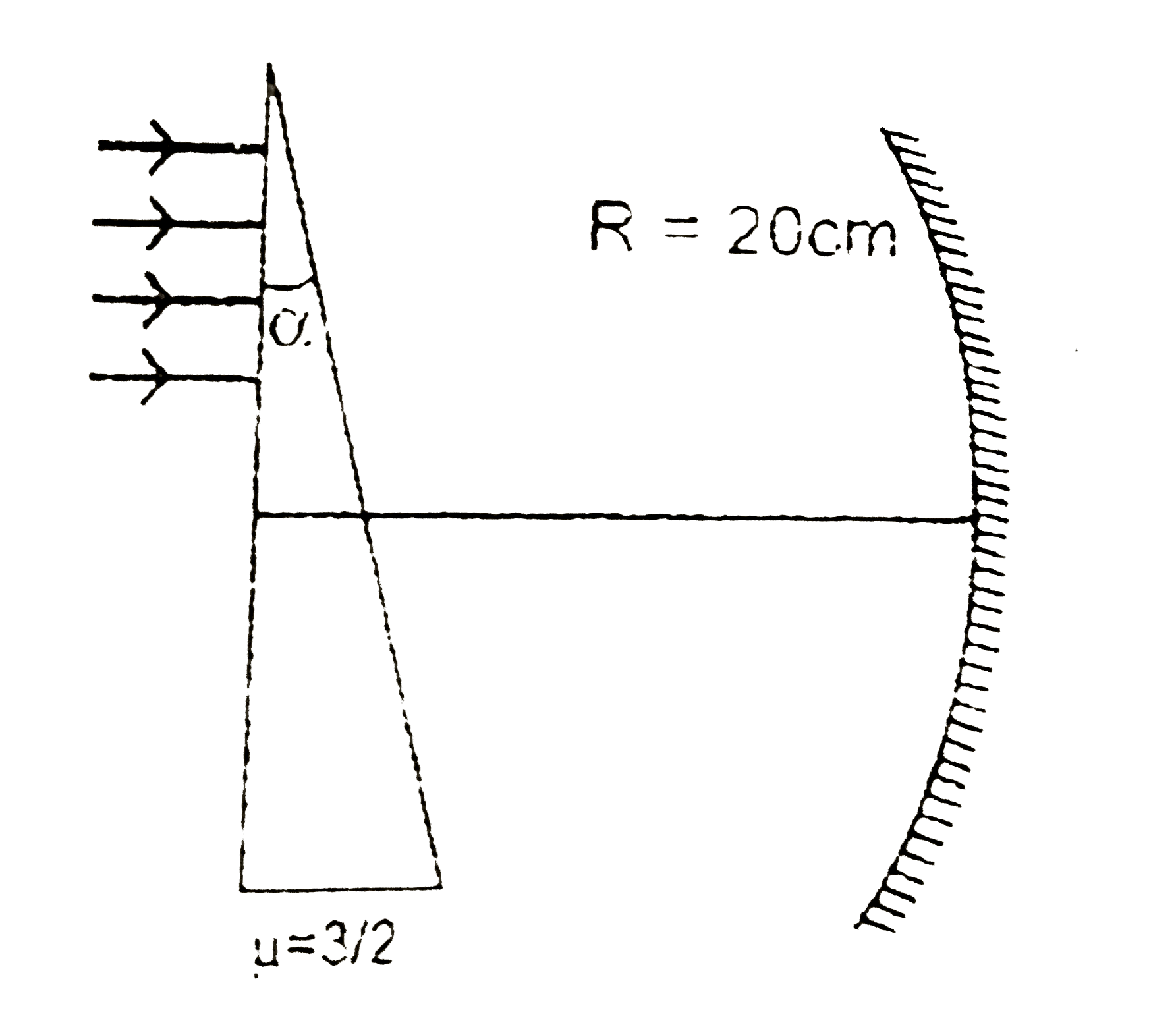
View SolutionIn the given figure a parallel beam of ligth is incident on the upper part of a prism of angle 1.8∘ and R.I.3/2 . The light coming out of the prism falls on a concave mirror of radius of curvature 20cm. The distance of the point (where the rays are focused after reflrction from the mirror) from the pricipal axis is: [use π=3.14]
View SolutionA beam of light coming from infinty is passing through a biconvex lens having radius of curvature R=20cm of each surface, if focused at a certain distance from lens. Find the radius of curvature of emergent wave front from lens : (μ≤ns=1.5)
View Solution

