In L-C oscillation, maximum charge on capacitor can be Q. If at any instant, electric energy and magnetic enegy associated with circuit is equal, then charge on capacitor at the anstant is
Q√2
Q2
√3Q2
3Q2
The correct Answer is:A
To solve the problem, we need to find the charge on the capacitor at the instant when the electric energy and magnetic energy in the LC circuit are equal. Here's a step-by-step solution:
Step 1: Understand the maximum charge and energy
The maximum charge on the capacitor is given as Q. The maximum energy stored in the capacitor can be calculated using the formula:
Umax=Q22C
where C is the capacitance.
Step 2: Set up the energy equations
At any instant, the electric energy (Ue) stored in the capacitor and the magnetic energy (Um) stored in the inductor are equal. Let's denote the charge on the capacitor at this instant as Q′. The electric energy at this instant is given by:
Ue=(Q′)22C
The magnetic energy in the inductor can also be expressed in terms of the current I. However, since we know that Ue=Um, we can express the total energy in the circuit as:
Utotal=Ue+Um
Step 3: Equate electric and magnetic energy
Since Ue=Um, we can write:
Ue=Um=(Q′)22C
Thus, we can express the total energy as:
Utotal=2Ue=2⋅(Q′)22C=(Q′)2C
Step 4: Relate total energy to maximum energy
The total energy in the LC circuit is also equal to the maximum energy, which we established as:
Utotal=Umax=Q22C
Step 5: Set the equations equal
Now we can set the two expressions for total energy equal to each other:
(Q′)2C=Q22C
Step 6: Simplify the equation
We can multiply both sides by C to eliminate the capacitance:
(Q′)2=Q22
Step 7: Solve for Q′
Taking the square root of both sides gives us:
Q′=Q√2
Conclusion
Thus, the charge on the capacitor at the instant when the electric energy and magnetic energy are equal is:
Q′=Q√2
---
The maximum charge on the capacitor is given as Q. The maximum energy stored in the capacitor can be calculated using the formula:
Umax=Q22C
where C is the capacitance.
At any instant, the electric energy (Ue) stored in the capacitor and the magnetic energy (Um) stored in the inductor are equal. Let's denote the charge on the capacitor at this instant as Q′. The electric energy at this instant is given by:
Ue=(Q′)22C
The magnetic energy in the inductor can also be expressed in terms of the current I. However, since we know that Ue=Um, we can express the total energy in the circuit as:
Utotal=Ue+Um
Since Ue=Um, we can write:
Ue=Um=(Q′)22C
Thus, we can express the total energy as:
Utotal=2Ue=2⋅(Q′)22C=(Q′)2C
The total energy in the LC circuit is also equal to the maximum energy, which we established as:
Utotal=Umax=Q22C
Now we can set the two expressions for total energy equal to each other:
(Q′)2C=Q22C
We can multiply both sides by C to eliminate the capacitance:
(Q′)2=Q22
Taking the square root of both sides gives us:
Q′=Q√2
Thus, the charge on the capacitor at the instant when the electric energy and magnetic energy are equal is:
Q′=Q√2
Similar Questions
Knowledge Check
The circuit is in a steady state.
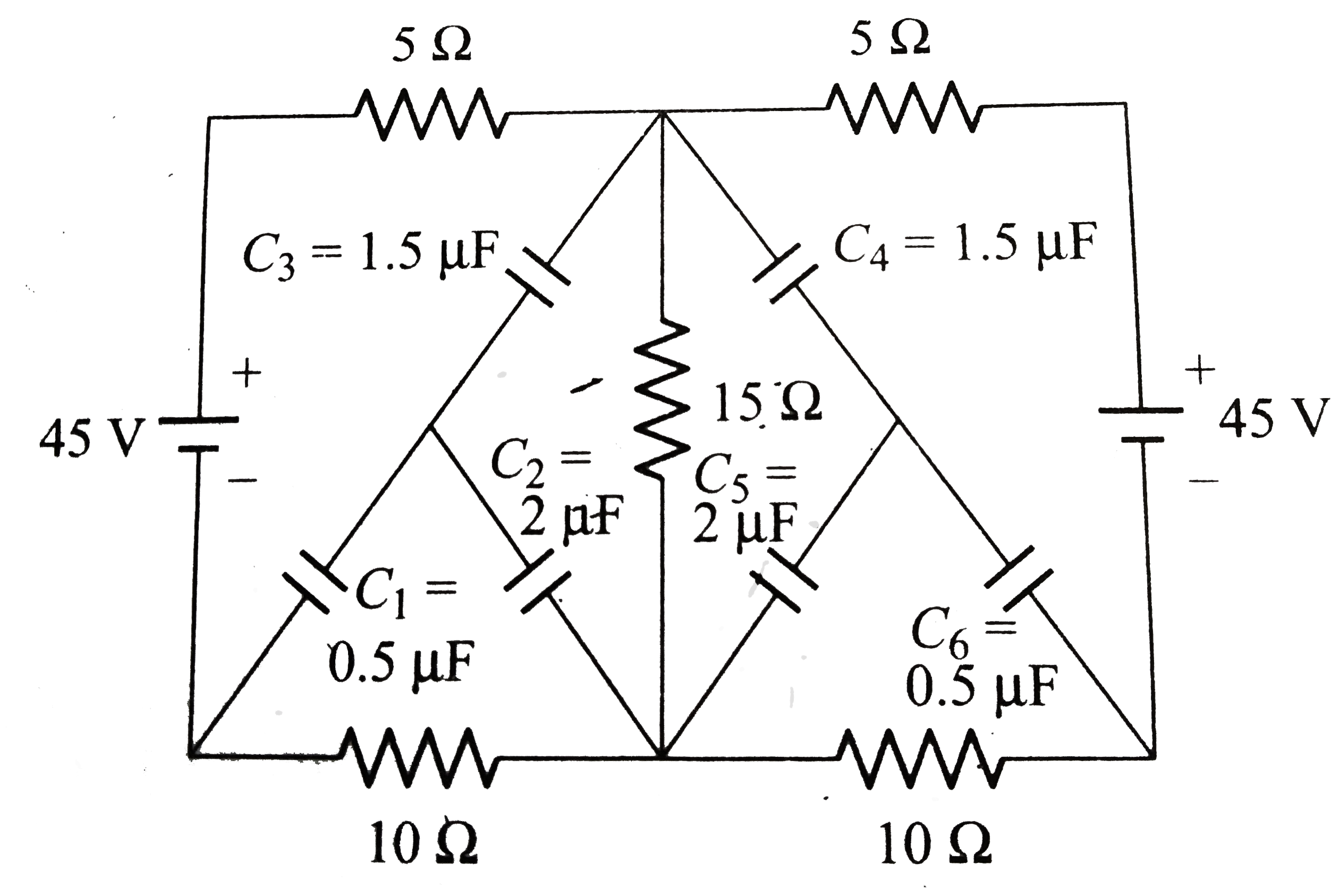
The charge in capacitor C3 isA10μCB30μCC20μCD40μCThe circuit is in a steady state.
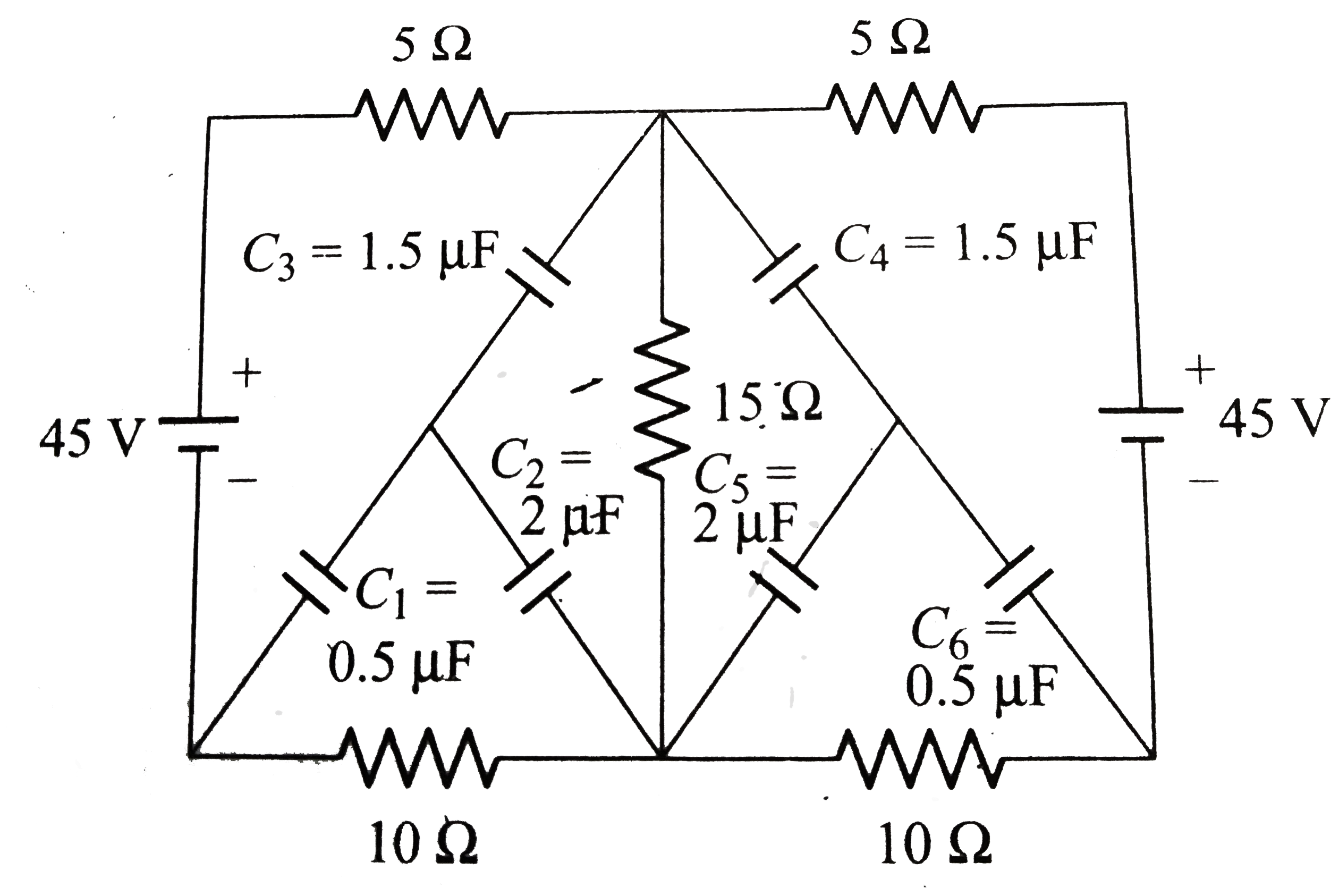
The charge in capacitor C2 isA30μCB10μCC20μCD40μCThe circuit is in a steady state.
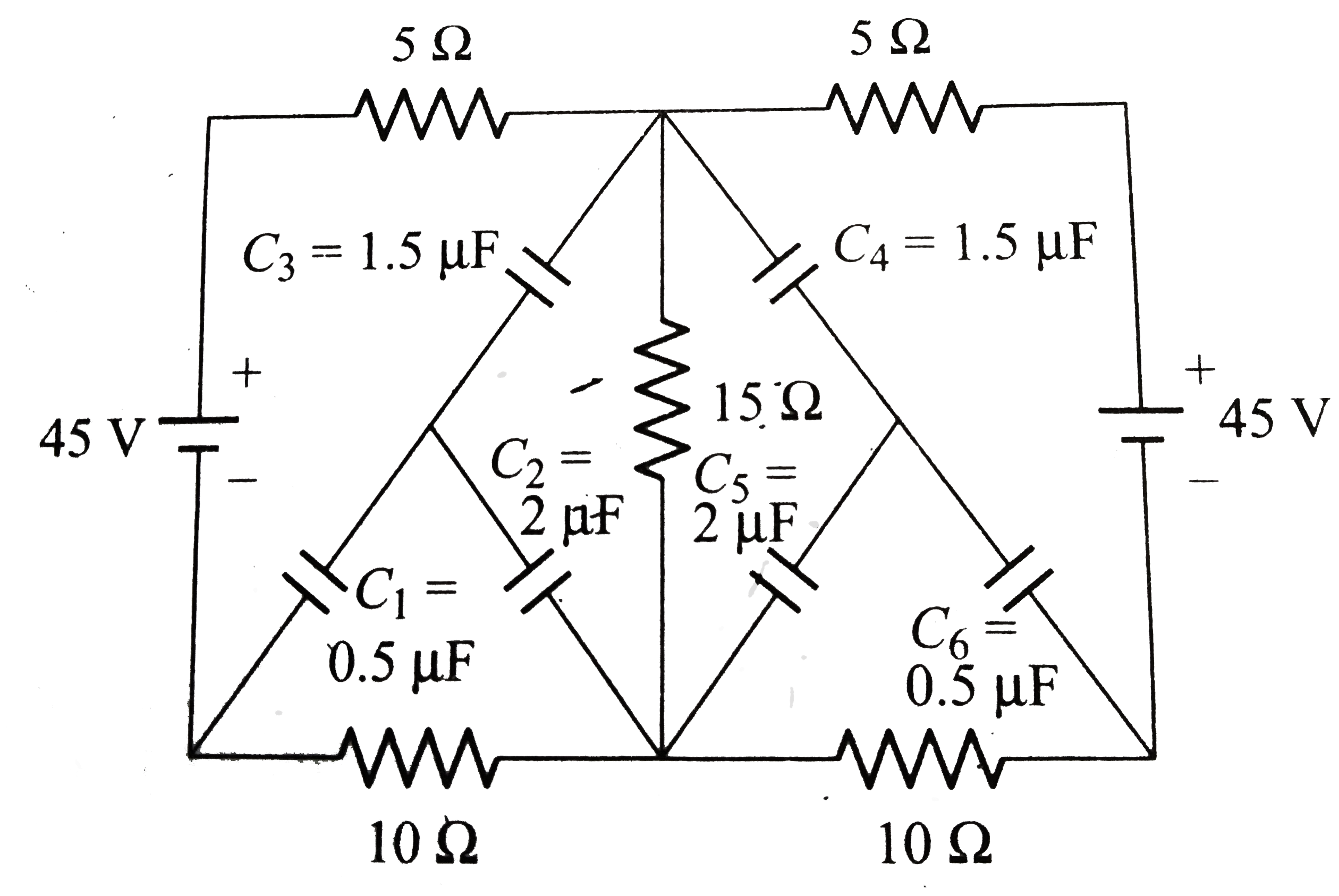
The charge in capacitor C1 isA20μCB30μCC40μCD10μC
A charged 8mF capacitor having charge 5mC is connected to a 5mH inductor. What is :
iv) the magnetic energy in the inductor at the instant when charge on capacitor is 4mC?
View SolutionThe capacitance of a charged capacitor is C and the energy stored in it is U. What is the value of charge on the capacitor?
View SolutionIn LC oscillations of a capacitor with an initial charge q0 is connected in parallel.
View SolutionIn the circuit shown in, C=6μF. The charge stored in the capacitor of capacity C is
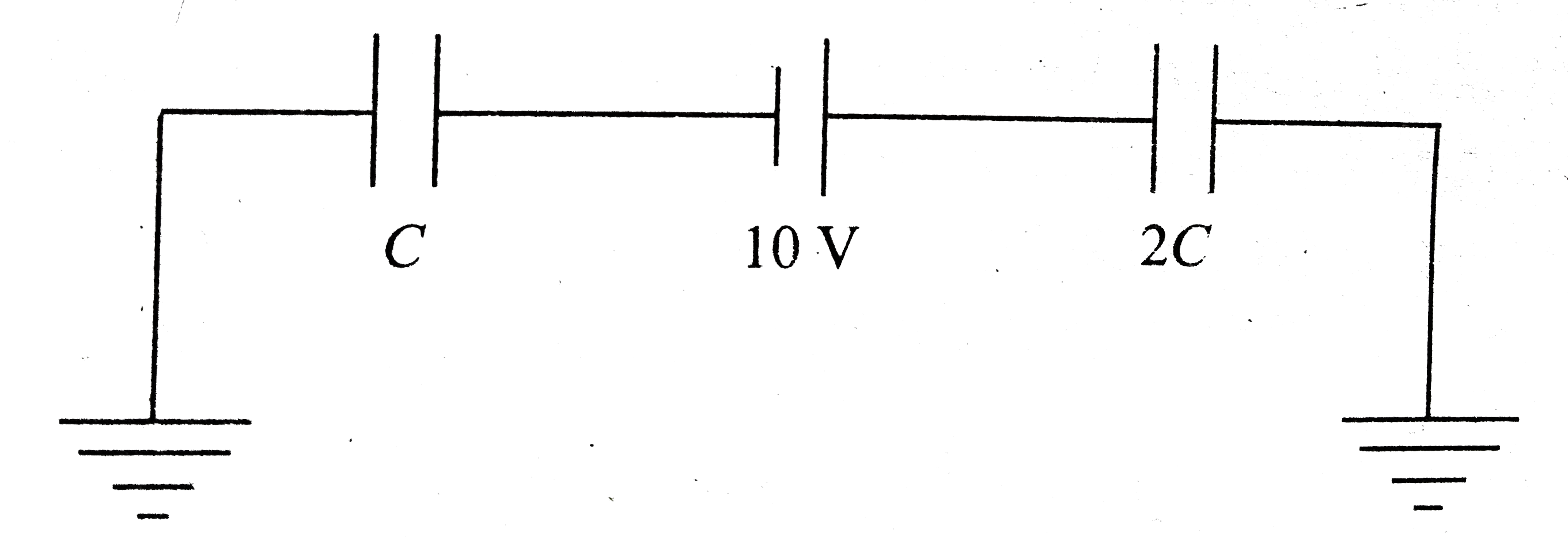 .
.
View SolutionIn an oscillating LC circuit the maximum charge on the capacitor is Q. The charges on the capacitor when the energy is stored equally between the electric and magnetic field is
View Solution