Two SHM's with same amplitude and time period, when acting together in perpendicular directions with a phase difference of π2 give rise to
Straight motion
Elliptical motion
Circular motion
None of these
The correct Answer is:C
To solve the problem, we need to analyze the situation where two simple harmonic motions (SHMs) with the same amplitude and time period are acting together in perpendicular directions with a phase difference of π2.
1. Define the SHM Equations:
Let the first SHM be represented by:
x(t)=Asin(ωt)
where A is the amplitude and ω is the angular frequency.
2. Define the Second SHM:
The second SHM, which is acting in a perpendicular direction with a phase difference of π2, can be represented as:
y(t)=Asin(ωt+π2)
3. Simplify the Second SHM:
Using the trigonometric identity sin(θ+π2)=cos(θ), we can rewrite the second SHM as:
y(t)=Acos(ωt)
4. Relate x and y:
We now have:
x(t)=Asin(ωt)
y(t)=Acos(ωt)
To find the relationship between x and y, we can use the Pythagorean identity:
sin2(θ)+cos2(θ)=1
5. Express the Pythagorean Identity:
Dividing both equations by A2:
(xA)2+(yA)2=sin2(ωt)+cos2(ωt)=1
6. Final Equation:
Rearranging gives us:
x2+y2=A2
This equation represents a circle with a radius A centered at the origin.
7. Conclusion:
The two SHMs combine to produce circular motion in the xy-plane, where the radius of the circular path is equal to the amplitude A.
Final Answer:
The two SHMs give rise to circular motion.
Let the first SHM be represented by:
x(t)=Asin(ωt)
where A is the amplitude and ω is the angular frequency.
The second SHM, which is acting in a perpendicular direction with a phase difference of π2, can be represented as:
y(t)=Asin(ωt+π2)
Using the trigonometric identity sin(θ+π2)=cos(θ), we can rewrite the second SHM as:
y(t)=Acos(ωt)
We now have:
x(t)=Asin(ωt)
y(t)=Acos(ωt)
To find the relationship between x and y, we can use the Pythagorean identity:
sin2(θ)+cos2(θ)=1
Dividing both equations by A2:
(xA)2+(yA)2=sin2(ωt)+cos2(ωt)=1
Rearranging gives us:
x2+y2=A2
This equation represents a circle with a radius A centered at the origin.
The two SHMs combine to produce circular motion in the xy-plane, where the radius of the circular path is equal to the amplitude A.
The two SHMs give rise to circular motion.
Topper's Solved these Questions
- OSCILLATIONSBOOK - AAKASH INSTITUTECHAPTER - OSCILLATIONSEXERCISE - Assignment (Section D) (ASSERTION-REASON TYPE QUESTIONS)
13 Videos
- OSCILLATIONSBOOK - AAKASH INSTITUTECHAPTER - OSCILLATIONSEXERCISE - Assignment (Section - B) (OBJECTIVE TYPE QUESTIONS)
30 Videos
- NUCLEIBOOK - AAKASH INSTITUTECHAPTER - NUCLEIEXERCISE - ASSIGNMENT (SECTION-D)
10 Videos
- PHYSICAL WORLDBOOK - AAKASH INSTITUTECHAPTER - PHYSICAL WORLDEXERCISE - ASSIGNMENT (Section-B)
5 Videos
Similar Questions
Discuss analytically the composition of two linear SHMs of the same period and along the sameline. Find the resultant amplitude when the phase difference is (1)zero (2) π3 (3) π2rad (4) π rad
View Solution(a) A particle is subjected to two SHMs of same time period in the same direction. If A1=6cm, A2=8cm, find the resultant amplitude if the phase difference between the motions is (a) 0∘, (b) 60∘, (c) 90∘ and (d) 120∘.
(b) In the previous problem if A1=A2=a and resultant amplitude is also a, find phase difference between them.
(c) Three SHMs of equal amplitude A and equal time periods in the same direction combine. The phase of the second motion is 120∘ ahead of first and the phase of the third motion is 120∘ ahead of the second. Find the amplitude of the resultant motion.
View Solution
Knowledge Check
Two particles execute SHM of same amplitude and same time period, about same mean position but with a phase difference between them. At an instant they are found to cross each other at x=+A3. The phase difference between them is
A2cos−1(15)B2sin−1(15)C2cos−1(13)D2sin−1(15)When two particles performing SHM of same amplitude and frequency arriving at a point of medium simultaneously with phase difference of π/2, then the resultant path is
AparabolicBellipticalCcircleDstraight lineTwo particles execute SHM of same amplitude of 20cm with same period along the same line about the same equilibrium position. If phase difference is π/3 then the maximum distance between these two will be
A10cmB20cmC10√2cmD20√2cm
A: The phase difference between the two particles shown below is π. (Assuming both particles have same time periods and same amplitudes).
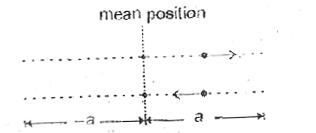
R: If the particles cross each other while they move in the opposite direction, they have a phase difference of π radian.
View SolutionTwo waves of same frequency but of amplitude a and 2a respectively superimpose over each other. The intensity at a point where the phase difference is 3π2, will be proportional to :
View SolutionThe equation of S.H.M. with amplitude 4m and time period 1/2 s with initial phase π/3 is x =
View SolutionThree SHO's of equal amplitude A and equal time period combine in the same direction. The difference in phase between successive SHO's os 60∘ahead of the other. The amplitude of the resultant oscillation is
View SolutionTwo waves having the same wave length and amplitude but having a constant phase difference but having a constant phase difference with time are known as
View Solution
