What will be the time period of a pendulum which beats seconds ( i.e.,it passes through the mean position after every one second ) it its length is doubled ?
Hint ....(i)
Fin using equation (i)
....(i)
Find using equation (i)
Topper's Solved these Questions
- OSCILLATIONSBook:AAKASH INSTITUTEChapter:OSCILLATIONSExercise:ASSIGNMENT ( SECTION -A)
Explore 58 Videos
- OSCILLATIONSBook:AAKASH INSTITUTEChapter:OSCILLATIONSExercise:ASSIGNMENT (SECTION-B )
Explore 25 Videos
- OSCILLATIONSBook:AAKASH INSTITUTEChapter:OSCILLATIONSExercise:Assignment (Section D) (ASSERTION-REASON TYPE QUESTIONS)
Explore 13 Videos
- NUCLEIBook:AAKASH INSTITUTEChapter:NUCLEIExercise:ASSIGNMENT (SECTION-D)
Explore 10 Videos
- PHYSICAL WORLDBook:AAKASH INSTITUTEChapter:PHYSICAL WORLDExercise:ASSIGNMENT (Section-B)
Explore 5 Videos
Similar Questions
What are the variables in the formula T=2π√lg?
View SolutionThe acceleration due to gravity on the surface of earth is 9.8ms−2.Time period of a simple pendulum on earth and moon are 3.5 second and 8.4 second respectively. Find the acceleration due to gravity on the moon .
Hint :Te=2π√LgeTm=2π√Lgm
T2eT2m=gmge
gm=T2eT2mge
View Solution
Knowledge Check
If the time period of a pendulum is 1sec, then what is the length of the pendulum at point of intersection of l−T and l−T2 graph.
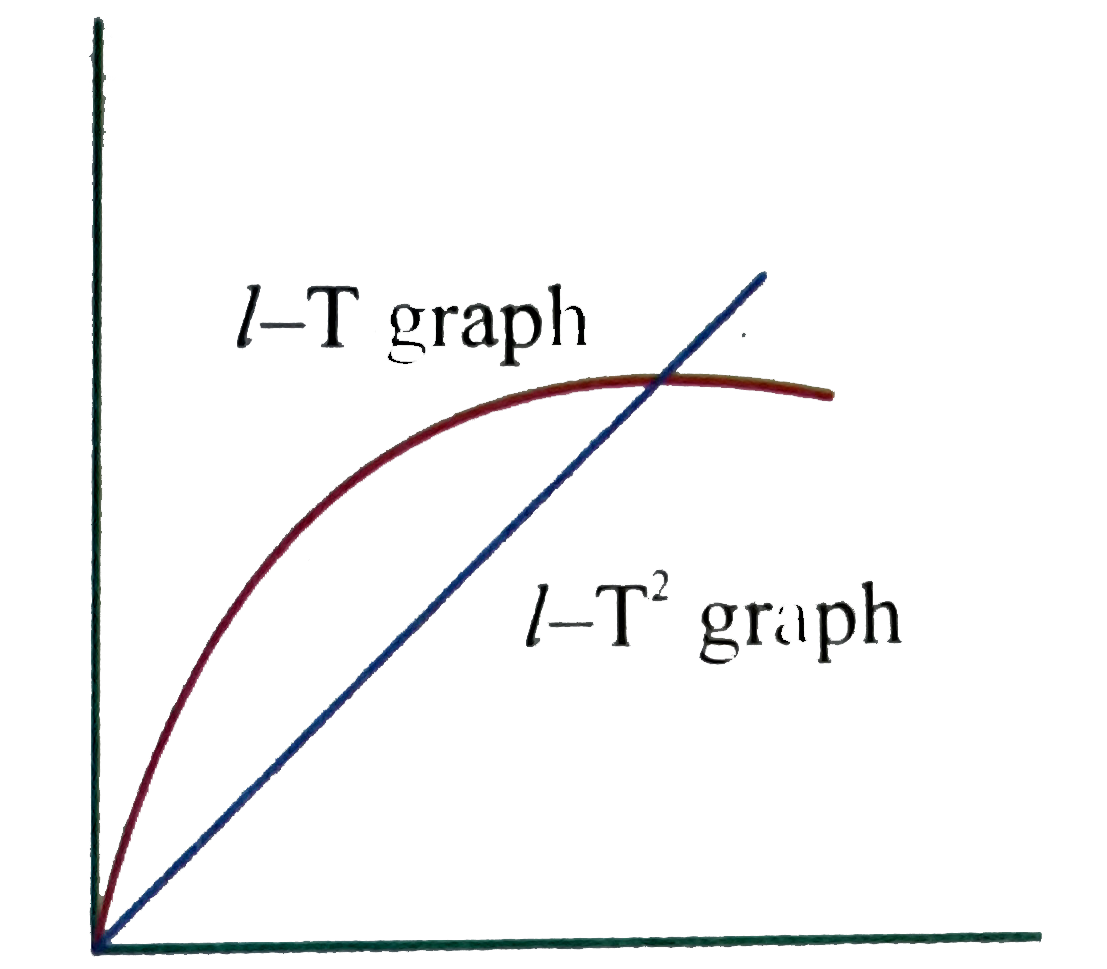 A25cmB21cmC22cmD27cm
A25cmB21cmC22cmD27cmIf the time period of a simple pendulum is T=2π√l/g , then the fractional error in acceleration due to gravity is
A4π2ΔlΔT2BΔll−2ΔlTCΔll+2ΔTTDNone of theseStatement-1: The time period of a simple pendulum on a satellite orbiting the earth is infinity
Because
Statement-2: Effective value of g in orbiting satellite is zero and T=2π√lgAStatement-1 is True, Statement-2 is true, Statement -2 is a correct explanation for statement-1BStatement-1 is true, statement-2 is true, statement-2 is not a correct explanation for statement-1CStatement-1 is true, Statement -2 is falseDStatement -1 is false, statement-2 is true
In the formula T=2π√lg,T is ____proportional to √l.
View SolutionThe time period of a simple pendulum of length 1 m is _____ second. ( take π2=10.g=10ms−2)
View SolutionShow that the expression of the time period T of a simple pendulum of length l given by T=2π√lg is dimensionally currect
View SolutionA simple pendulum has length L and period T. As it passes through its equilibrium position, the string is suddenly clamped at its midpoint. The period then becomes
View SolutionThe time period of a pendulum of length 'l' and mass of the bob 'm' is T. Time period of a pendulum with mass of the bob 2m and length l is ______.
View Solution

