A: If the force of gravitation in inversely proportional to the distance r rather than given by Newton , then orbital velocity of the satellite around the earth is independent of r .
R : so , hence independent of r .
If both Assertion & Reason are true . And the reason is the correct explanation of the assertion , then mark (1)
If both Assertion & Reason are true but the reason is not the correct explanation of the assertion , then mark (2)
If Assertion is true statement but Reason is false , then mark (3)
It will move the same speed , tangentially to the spacecraft
The correct Answer is:A
To solve the problem, we need to analyze the gravitational force and the orbital velocity of a satellite under the assumption that the gravitational force is inversely proportional to the distance r instead of r2.
1. Understanding the Gravitational Force:
The gravitational force Fg acting on a satellite of mass m in orbit around the Earth (mass M) is given by the new assumption:
Fg=kr
where k is a constant.
2. Centripetal Force Requirement:
For the satellite to maintain circular motion, the gravitational force must provide the necessary centripetal force. The centripetal force Fc required for circular motion is given by:
Fc=mv2r
where v is the orbital velocity of the satellite.
3. Setting Up the Equation:
Since the gravitational force provides the centripetal force, we can equate the two forces:
mv2r=kr
4. Cancelling r:
We can multiply both sides by r (assuming r≠0):
mv2=k
5. Solving for Orbital Velocity:
Rearranging the equation gives us:
v2=km
Taking the square root of both sides, we find:
v=√km
Here, k and m are constants, meaning that v is independent of r.
6. Conclusion:
Thus, under the assumption that the gravitational force is inversely proportional to r, the orbital velocity v of the satellite does not depend on the radius r of its orbit.
The gravitational force Fg acting on a satellite of mass m in orbit around the Earth (mass M) is given by the new assumption:
Fg=kr
where k is a constant.
For the satellite to maintain circular motion, the gravitational force must provide the necessary centripetal force. The centripetal force Fc required for circular motion is given by:
Fc=mv2r
where v is the orbital velocity of the satellite.
Since the gravitational force provides the centripetal force, we can equate the two forces:
mv2r=kr
We can multiply both sides by r (assuming r≠0):
mv2=k
Rearranging the equation gives us:
v2=km
Taking the square root of both sides, we find:
v=√km
Here, k and m are constants, meaning that v is independent of r.
Thus, under the assumption that the gravitational force is inversely proportional to r, the orbital velocity v of the satellite does not depend on the radius r of its orbit.
Topper's Solved these Questions
- GRAVITATION Book:AAKASH INSTITUTEChapter:GRAVITATION Exercise:ASSIGNMENT SECTION - C (PREVIOUS YEARS QUESTIONS)
Explore 52 Videos
- ELECTROSTATIC POTENTIAL AND CAPACITANCE Book:AAKASH INSTITUTEChapter:ELECTROSTATIC POTENTIAL AND CAPACITANCE Exercise:ASSIGNMENT SECTION - D
Explore 13 Videos
- KINETIC THEORYBook:AAKASH INSTITUTEChapter:KINETIC THEORYExercise:EXERCISE (ASSIGNMENT) SECTION - D Assertion - Reason Type Questions
Explore 10 Videos
Similar Questions
If gravitational forces between a planet and a satellite is proportional to R−5/2. If R is the orbit radius. Then the period of revolution of satellites is proportional to Rn. Find n.
View SolutionSuppose the gravitational force varies inversely as the nthpower of distance. Then the time period of a planet in circular orbit of radius R around the sun will be proportional to-
View Solution
Knowledge Check
If ve denotes escape velocity and V0 denotes orbital velocity of a satellite revolving around a planet of radius R, then
Ave=√2⋅voBve=2voC2ve=voD√2⋅ve=voThe graph that represents the relation between orbital velocity (v0) of a satellite and radius (r) of the orbit around earth is
A B
B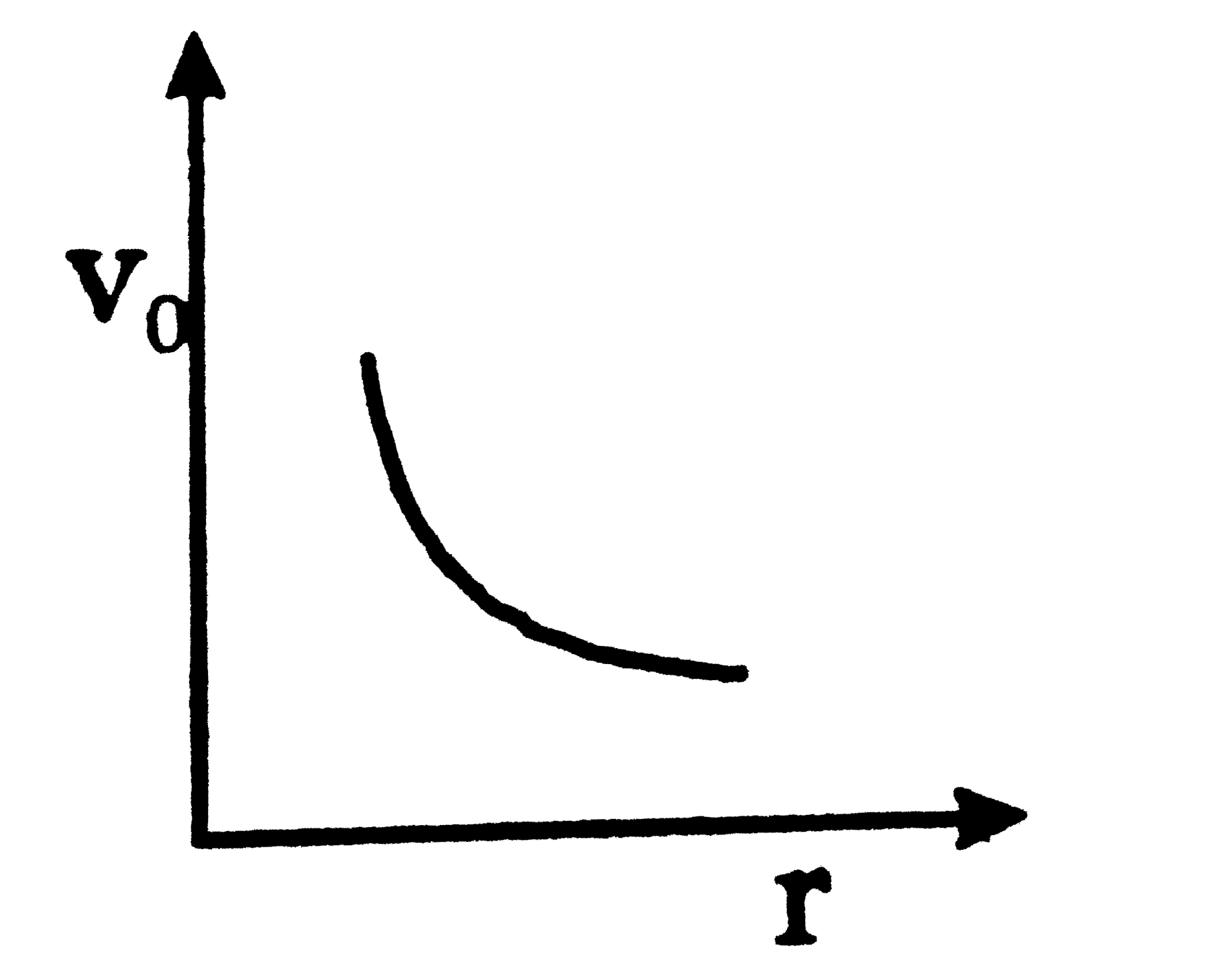 C
C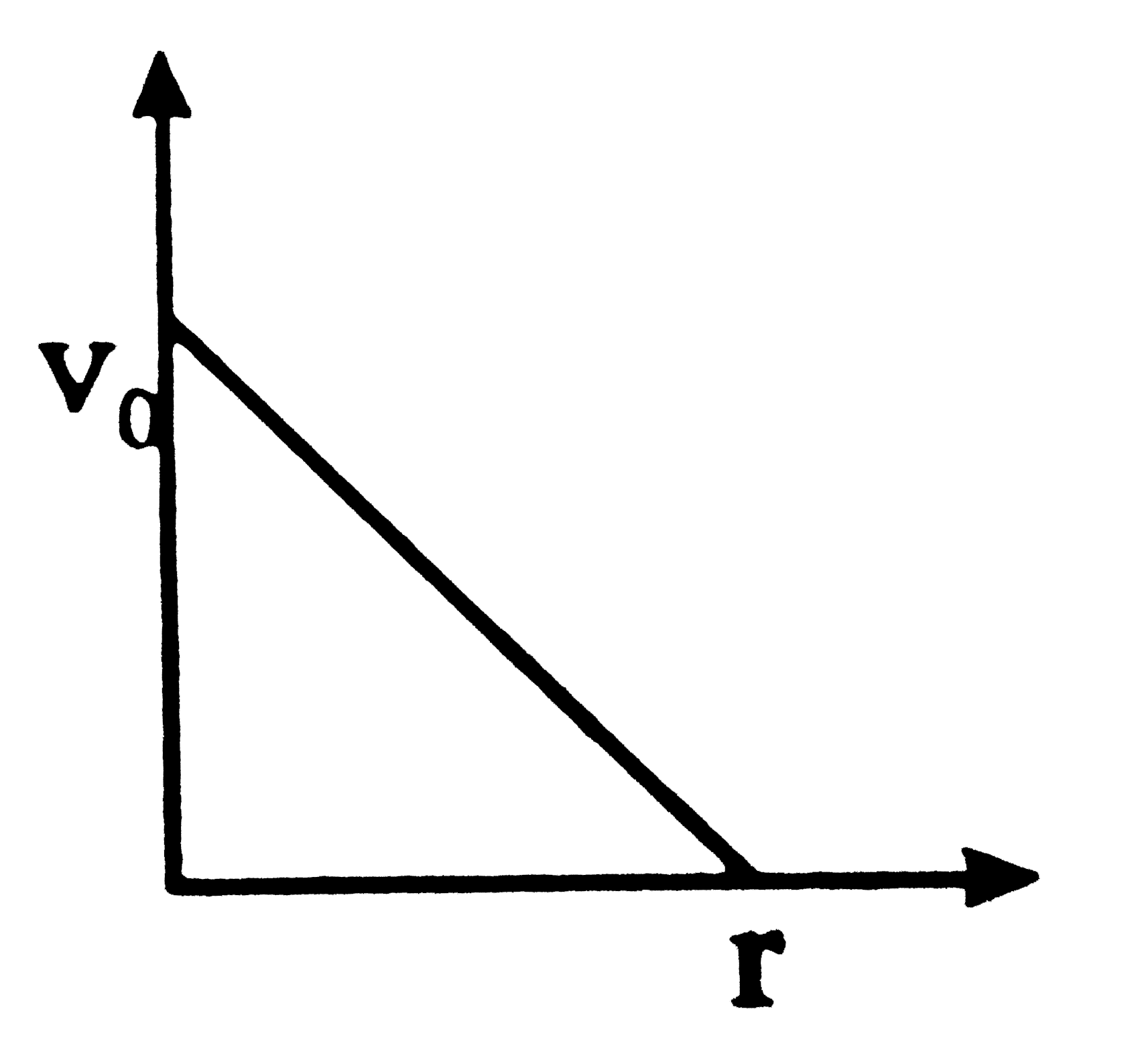 D
D
Suppose the gravitational force varies inversely as the nth power of distance. Then the time period of a planet in circular orbit of radius 'R' around the sun will be proportional to
ARnBRn−12CRn+12DRn−22
If mass density of earth varies with distance 'r' from centre of earth as ρ=krand'R'isradius of earth, then find the orbital velocity of an object revolving around earth at adistance '2R' from its centre.
View SolutionRadius of orbit of satellite of earth is R. Its kinetic energy is proportional to
View SolutionSatellites A and B are orbiting around the earth in orbits of ratio R and 4R respectively. The ratio of their areal velocities is-
View SolutionTwo identical satellites are orbiting are orbiting at distances R and 7R from the surface of the earth, R being the radius of the earth. The ratio of their
View SolutionThe radii of circular orbits of two satellite A and B of the earth are 4R and R, respectively. If the speed of satellite A is 3v, then the speed of satellite B will be
View Solution
